Statistical Power to Detect Genetic (Co)Variance of Complex Traits Using SNP Data in Unrelated Samples
Genome-wide association studies (GWAS) have identified thousands of genetic variants for hundreds of traits and diseases. However, the genetic variants discovered from GWAS only explained a small fraction of the heritability, resulting in the question of “missing heritability”. We have recently developed approaches (called GREML) to estimate the overall contribution of all SNPs to the phenotypic variance of a trait (disease) and the proportion of genetic overlap between traits (diseases). A frequently asked question is that how many samples are required to estimate the proportion of variance attributable to all SNPs and the proportion of genetic overlap with useful precision. In this study, we derive the standard errors of the estimated parameters from theory and find that they are highly consistent with those observed values from published results and those obtained from simulation. The theory together with an online application tool will be helpful to plan experimental design to quantify the missing heritability, and to estimate the genetic overlap between traits (diseases) especially when it is unfeasible to have the traits (diseases) measured on the same individuals.
Published in the journal:
. PLoS Genet 10(4): e32767. doi:10.1371/journal.pgen.1004269
Category:
Research Article
doi:
https://doi.org/10.1371/journal.pgen.1004269
Summary
Genome-wide association studies (GWAS) have identified thousands of genetic variants for hundreds of traits and diseases. However, the genetic variants discovered from GWAS only explained a small fraction of the heritability, resulting in the question of “missing heritability”. We have recently developed approaches (called GREML) to estimate the overall contribution of all SNPs to the phenotypic variance of a trait (disease) and the proportion of genetic overlap between traits (diseases). A frequently asked question is that how many samples are required to estimate the proportion of variance attributable to all SNPs and the proportion of genetic overlap with useful precision. In this study, we derive the standard errors of the estimated parameters from theory and find that they are highly consistent with those observed values from published results and those obtained from simulation. The theory together with an online application tool will be helpful to plan experimental design to quantify the missing heritability, and to estimate the genetic overlap between traits (diseases) especially when it is unfeasible to have the traits (diseases) measured on the same individuals.
Introduction
Genome-wide association studies (GWAS) have been extremely successfully in identifying genetic variants associated with complex traits and diseases in humans [1]. In GWAS, hundreds of thousands or millions of SNPs are tested one by one for statistical evidence of association with a trait, and to avoid false positive discoveries due to the very large number of statistical tests being conducted, usually a very stringent p-value threshold, e.g. 5×10−8, is used to report a significant finding. Therefore, if there are many genes each with a small effect affecting the trait, most of these genetic variants will fail to pass the stringent threshold and remain undetected. This is one of the explanations of the ‘missing heritability’ question, that genetic variants identified from GWAS so far explain a fraction of the heritability for complex traits [2]. We proposed a method, which is able to estimate the total amount of variance explained by all SNPs together without testing the SNPs individually for a quantitative trait [3], and subsequently extended it to the estimation of missing heritability for binary disease data from ascertained case-control studies [4]. The analyses until recently only included common SNPs (e.g. minor allele frequency >0.01). The estimate quantifies the overall contribution from the additive effects of all SNPs, which is the upper limit of the proportion of variance that is captured by the additive effects of the set of SNPs used in the estimation, and is also the lower limit of the narrow-sense heritability of the trait. We also extended the method to estimate the genetic correlation between two traits using SNP data [5], [6]. In contrast to the traditional (co)variance estimation methods that rely on pedigree information (family/twin studies), our method uses unrelated samples from a general population and the genetic (co)variance is estimated using a genetic relationship matrix (GRM) estimated from SNPs. The estimate of genetic variance using SNP data in unrelated individuals is free of confounding from common environment effects shared between close relatives that are difficult to model in family-based analyses, and is directly comparable to results from GWAS, because both are based on the same experimental design. For multiple trait analysis, the SNP-based approach allows the estimation of the genetic correlation between complex traits measured on different samples [6], [7]_ENREF_8. This is important in particular for estimating the genetic correlation between diseases because multiple diseases are unlikely to co-segregate in sufficiently large pedigrees to allow estimation using traditional pedigree design. The SNP-based method has the flexibility of estimating the genetic correlation between any two diseases using completely independent case-control data. Other methods to estimate genetic parameters from individual-level or summary GWAS data have also been reported [8]–[10].
We previously named the SNP-based method mentioned GREML [11], as a complement to GBLUP [12] where variance components are assumed known, and have been implemented them in the software tool GCTA [13]. One outstanding question is the statistical power of detecting genetic variation using the population-based estimation method, for example how many samples are required to achieve estimates that are sufficiently accurate to detect genetic (co)variance of complex traits. In this paper, we derive the sampling variance of the estimate of genetic (co)variance by analytical derivations and verify our derivations by simulations under a range of scenarios. We also provide an online tool for power calculation.
Methods and Results
Univariate analysis
The methods of using SNP data to estimate genetic variance in unrelated individuals have been detailed elsewhere [3], [13]. In brief, given GWAS data, we can model the phenotype as
where y is an N×1 vector of phenotypes with N being the sample size, g is an N×1 vector with each of its elements being the total genetic effect of an individual captured by all SNPs, and e is an N×1 vector of residuals. We have and , where is the genetic variance captured by all SNPs, A is the genetic relationship matrix (GRM) estimated from SNPs [3], is the residuals variance and I is an identity matrix. The genetic relationships, also known as ‘genomic relationships’ or ‘genetic similarity relationships’, are referenced to the current population, and so can be negative as they are distributed about a mean of zero. Equation (1) is a typical mixed linear model with , in which the variance components can be estimated using a restricted maximum likelihood (REML) approach [13], [14]. The proportion of variance explained by all SNPs (SNP heritability) is defined as .For power calculation, we need to know the sampling variance of the estimate of , i.e. . In practice, the asymptotic sampling variance (standard error squared) of a variance component is calculated from a diagonal element of the inverse of the information matrix in maximum likelihood analysis [15]–[18]. Each element of the information matrix, however, comprises complex forms of matrix algebra including a matrix inverse. It is therefore unfeasible to derive directly from the inverse of the information matrix. We show below an equivalent approach to obtain under the simple regression framework.
For unrelated individuals, where the phenotypic correlation between individuals is small, mixed linear model analysis using the REML approach is asymptotically equivalent to simple regression analysis of pairwise phenotypic similarity/difference on pairwise genetic similarity, as measured by identity-by-descent (IBD) or identity-by-state (IBS) at genome-wide markers [17]–[20]. Under such circumstance, a regression of the cross-product of the phenotypes is equivalent to using both the squared difference and squared sum of the pairwise phenotypes, and using the cross-product is equivalent to using maximum likelihood [19]. The model for the regression-based analysis can be written as
where with and being the phenotypes of individuals i and j (), is the ij-th element of the GRM A, and is the residual of this regression. There are observations (contrasts) in the regression. The regression coefficient b is equivalent to because In such a simple regression, the sampling variance of the estimate of the regression coefficient is If the samples are unrelated and the phenotypes have been standardized with mean of 0 and variance of 1, then and . Since is small, there is hardly any variance in that can be explained by so that . We therefore have Under circumstances when is large, for example when the GRM is calculated from pedigree data, a substantial proportion of variance in could be explained by , so that will be smaller than and the sampling variance of estimate of genetic variance will be reduced accordingly. In general, and the residual variance in equation (2) depend on the number of SNP that are used to calculate the GRM and their correlation structure. Although can be calculated empirically from the data, theoretical work suggest it is approximately 2×10−5 for genome-wide coverage of common SNPs in human populations [21]. Since the phenotypic variance is usually estimated with very high precision, This suggests that the standard error (SE) of depends only on sample size, and is approximately . We show by simulations based on real genotype data (Text S1) that this approximation is very accurate (Figure 1 and Table S1). The SEs calculated from the approximation theory are also highly consistent with those reported from our previous studies for human height and body mass index (BMI). For example, the reported SE of for height was 0.083 using 3925 unrelated samples [3] and 0.029 for both height and BMI, irrespective to , using 11586 unrelated samples [22], and the SE calculated from the approximation theory is 0.081 for N = 3925 and 0.027 for N = 11586. 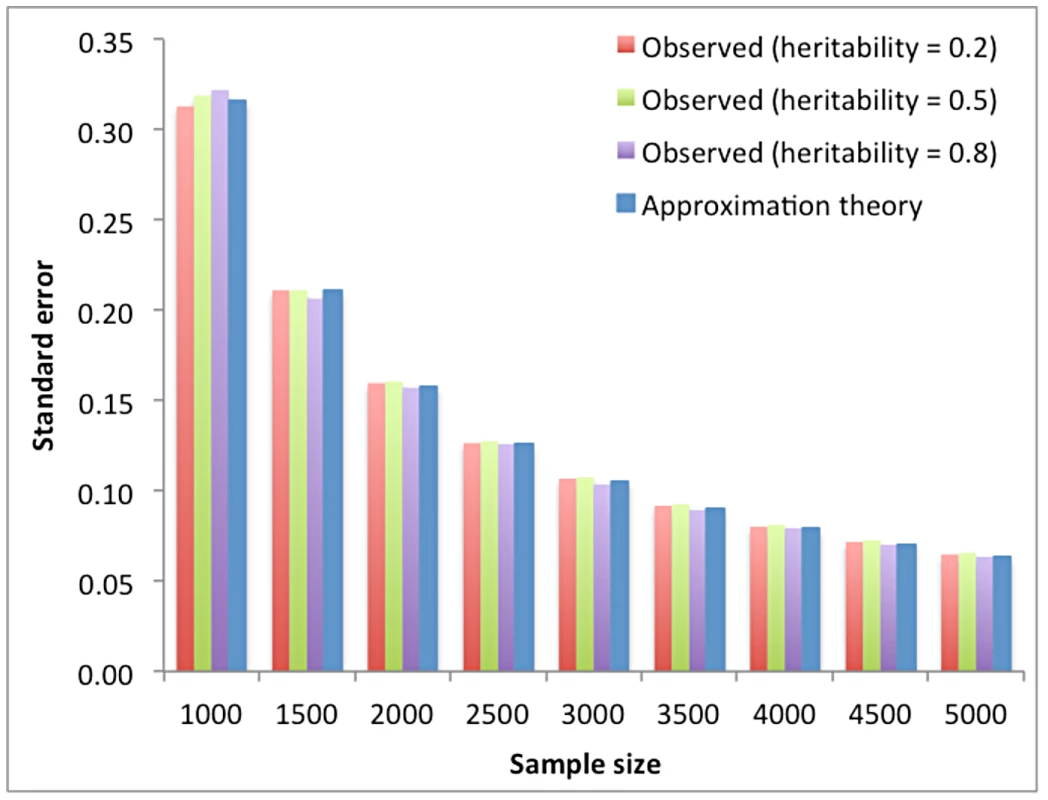
Bivariate analysis (traits measured on the same individuals)
For a bivariate analysis where the two traits are measured on the same individuals, the mixed linear model can be written as [6]
where y1 and y2 are N×1 vector of phenotypes, g1 and g2 are N×1 vectors of genetic effects with and , e1 and e2 are N×1 vectors of residuals with and , and N is the sample size. The variance covariance matrix is where is the genetic covariance between the two traits and is the residual covariance. The genetic variance and covariance components can also be estimated using REML [6]. The genetic correlation is estimated as . Since is a non-linear function of , and , there is no explicit derivation for . Reeve (1955) and Robertson (1959) provided an approximation of in the context of balanced pedigree design as [23], [24] and Koots and Gibson (1996) proposed a modified version as [25], where is the phenotypic correlation between the traits. However, both approximations have an unsatisfying property that will approach 0 if or is close to 1. We derived an approximation, which does not have this problem (Text S2), i.e. As described above, for a GRM estimated from common SNPs in unrelated individuals in human populations, therefore . When , i.e. the traits are completely independent, . We tested equation (7) by simulations based on real genotype data (Text S1). The simulation results suggest that the approximation is reasonably accurate (Table 1). For real data analysis, we previously estimated the genetic correlation between intelligence at age 11 years and in old age of 0.62 with a SE of 0.23 using 1729 samples [5], consistent with the predicted SE of 0.22 from the approximation theory. 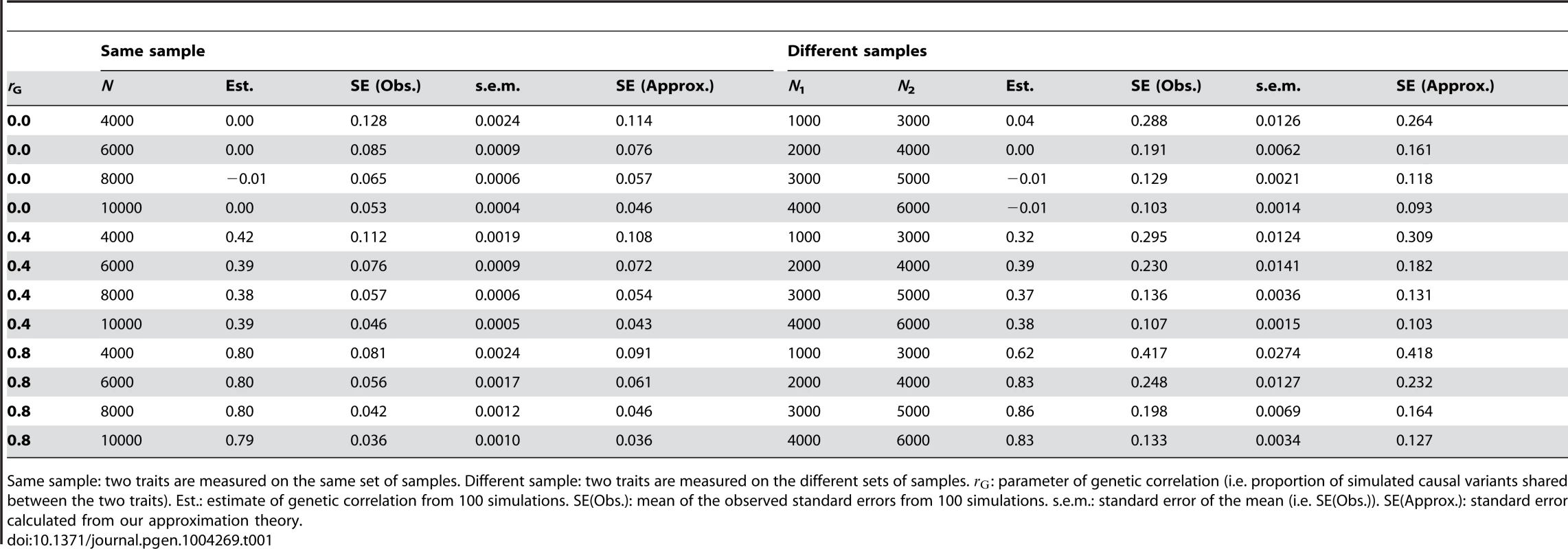
Bivariate analysis (traits measured on different sets of individuals)
For a bivariate analysis where the two traits are measured on different sets of individuals, e.g. height in males and blood pressure in females, the variance-covariance matrix is [6]
where y1 is an N1×1 vector of phenotypes in sample set #1 (e.g. males), and y2 is an N2×1 vector of phenotypes for in sample set #2 (e.g. females), with N1 and N2 being the sample sizes of the two sets. A1 is an N1×N1 GRM for individuals in sample set #1, A2 is an N2×N2 GRM in sample set #2 and A12 is an N1×N2 GRM between the two sets of samples. and are the genetic variance for the two traits. and are the residual variances with the corresponding identify matrix I1 and I2. is the genetic covariance between traits. Since the two traits are measured on different sets of samples, the residual covariance is ignored because it is assumed that there is no covariance between the unrelated individuals apart from that caused by genetic factors. The genetic correlation is also estimated as , however, the sampling variance of is different from that described above. Since the traits are measured in different sets of samples, . Therefore, from a second order Taylor series approximation [15] This approximation involves the sampling variance of . We show below an equivalent approach to obtain .Analogous to the univariate analysis, estimation of genetic covariance by a bivariate mixed linear model analysis is asymptotically equivalent to the following linear regression model
where i.e. the product of phenotypes between the i-th individual in set #1 and the j-th individual in set #2, and is the ij-th element of the GRM A12, i.e. the genetic relationship between the i-th individual in set 1 and the j-th individual in sample set #2. The regression coefficient is equivalent to genetic covariance between the two traits because If the two sample sets are independent and phenotypes for both traits have been standardized with mean of 0 and variance of 1, then and . Since is small, . We then have .We know from the derivations above that and . For unrelated individuals sampled from the same population, , we therefore get
This was also tested by simulations (Text S1) and the approximated standard errors were highly consistent with those observed from simulations, especially when sample size was large (Table 1). When , i.e. two traits are completely independent, for traits measured on the same sample, and for traits measured on different samples. Therefore, for independent traits, the ratio of sampling variance of genetic correlation between the two traits measured on the same sample to that on different samples is simply .Case-control studies
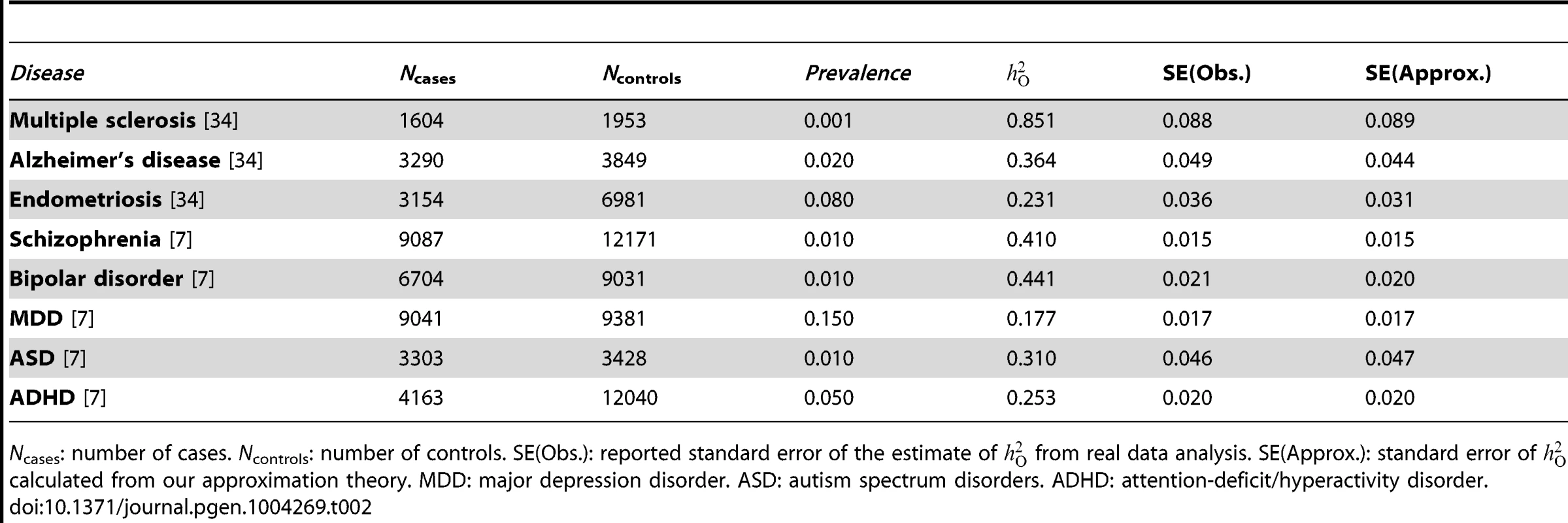
For case-control studies, the proportion of variance in case-control status (0 or 1) that is explained by all SNPs on the observed scale () can be estimated using a linear model [4]. Therefore, the same approximations to the sampling variance of genetic variance and genetic correlation for quantitative traits can be applied directly to case-control studies. As shown in equation (5), in a univariate analysis, the sampling variance of SNP-based heritability depends only on sample size and variance in genetic relatedness, independent of the properties of the phenotype, so that var() is also approximately in a case-control study with N being the total number of cases and controls. We show in Table 2 that the observed standard errors of the estimates of from published studies are highly consistent with those predicted from our approximation theory.
To calculate power, however, we would need to specify , which is a parameter with non-intuitive properties, and depends on the prevalence of the disease in the population (K), the proportion of variance in disease liability that is captured by the SNPs at population level, and the proportional of cases in the sample (v). For this reason we define as the variance explained by all SNPs at the population level on the unobserved underlying scale of disease liability, and use a linear transformation to transform to on the liability scale [4], i.e. and with . We then get
where Ncase is the number of cases, Ncontrol is the number of controls, and i is the selection intensity which is a function of K [4]. We illustrate in Figure 2 the dependency of the SE of on disease prevalence (K) and proportion of cases in the sample (v) due to the transformation. 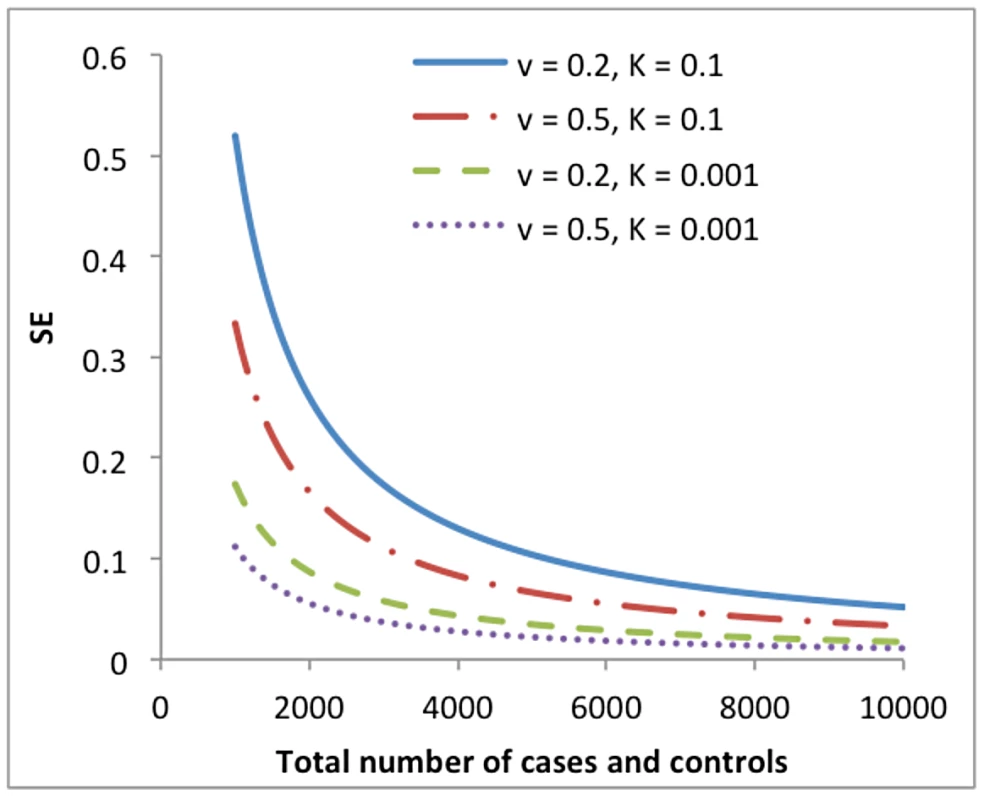
As shown in equation (10), in a bivariate analysis where traits are measured on different sets of samples, the sampling variance of genetic correlation depends on sample sizes, trait heritabilities and the genetic correlation parameter, which is also independent of the properties of the phenotypes. Therefore, in a bivariate analysis of two independent case-control disease studies,
where N1 and N2 are the total numbers of cases and controls of the two case-control studies, respectively. This also applies to a bivariate analysis of a quantitative trait and a cases-control disease study on different sets of samples, i.e. These two equations can also be expressed with respect to , given (see above). We show in Table 3 that the reported SEs of from bivariate analyses of psychiatric diseases are also highly in line with the predicted SEs from the approximation theory. ![Standard errors of the estimates of genetic correlations from published bivariate analyses of case-control studies for psychiatric diseases <em class="ref">[7]</em> vs. those predicted from the approximation theory.](https://www.prolekarniky.cz/media/cache/resolve/media_object_image_small/media/image/2f0eb38fde3d59aea42eba897c8eaf8d.png)
Statistical power
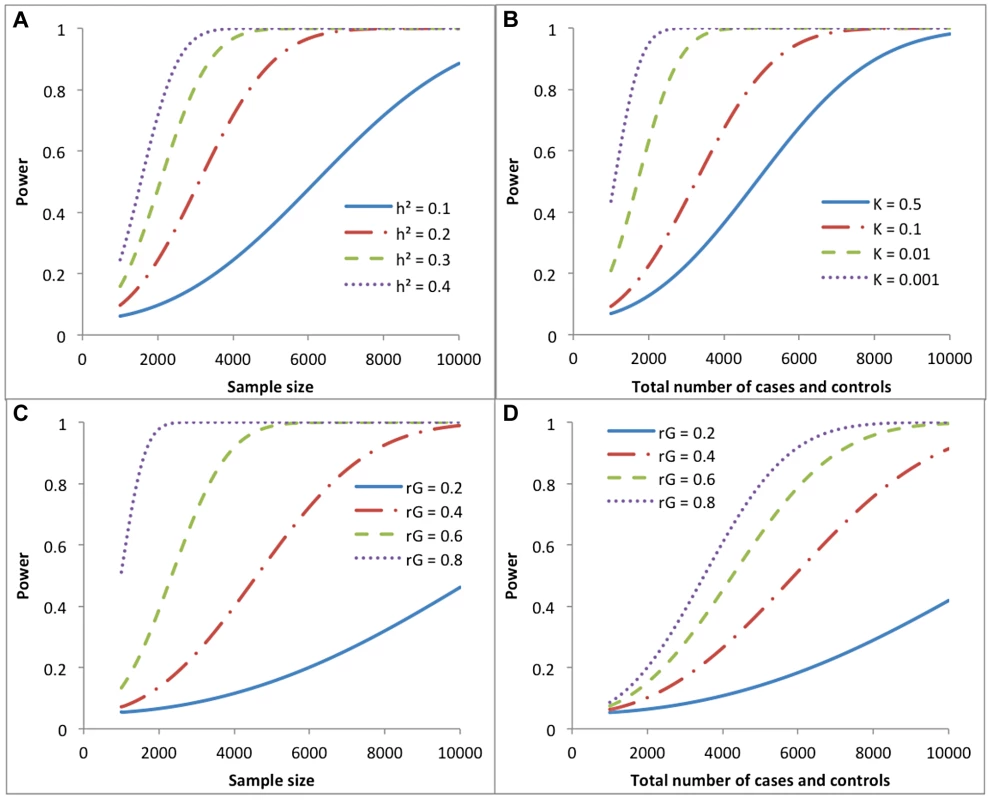
Statistical power is calculated from the population value of the parameter and its sampling variance, which was derived above. If the parameter is θ, where θ is either the proportion of phenotypic variance captured by SNPs () in the univariate case or the genetic correlation () in the bivariate case, then is asymptotically distributed as a non-central χ2 with 1 degree of freedom and non-centrality parameter (NCP) of . Given λ and the type-I error rate of α, statistical power is the probability that a non-central χ2 variable is larger than the central χ2 threshold that is determined by α. We show in Figure 3 the statistical power based on the sampling variance from our approximation theories to detect in a univariate case and in a bivariate case under a range of scenarios. For example, for a quantitative trait, approximately 8900, 4500, 3000 and 2300 independent individuals are required to detect of 0.1, 0.2, 0.3 and 0.4 with >80% power at a type-I error rate of 0.05, respectively. For two quantitative traits measured on the same sample, approximately 7000, 4700, 2500 and 1600 independent individuals are required to detect of 0.2, 0.4, 0.6 and 0.8 with >80% at a type-I error rate of 0.05, respectively.
Online tool
We have also developed an online calculator (GCTA Power Calculator, http://spark.rstudio.com/ctgg/gctaPower), as part of the GCTA [13] software package (http://ctgg.qbi.uq.edu.au/software/gcta), using R-Shiny (http://shiny.rstudio.org) to calculate the SE of genetic variance or genetic correlation and statistical power given user-defined parameters.
Discussion
We have derived the approximate sampling variance of the estimate of variance explained by all common SNPs () for a quantitative trait or case-control study of a disease, and genetic correlation () between two quantitative traits, between two diseases, or between a quantitative trait and a disease, using genome-wide SNP data in unrelated individuals. We believe that the derivations and the online tool will be helpful for researchers to determine how many samples are required to detect (or ) and to estimate (or ) with adequate precision before collecting the genotype data.
The sampling variance of for a complex trait is inversely proportional to sample size (N) and the variance in SNP-based genetic relatedness (), and independent of . The sampling variance of between two complex traits is a function of , N of the two samples, of the two traits and when the traits are measured on different samples, and further depends on the phenotypic correlation () when traits are measured on the same samples. All the approximation theories apply to case-control studies of diseases since the case-control data can be analysed using a linear model on the observed 0–1 scale. The sampling variance for the estimate on the observed scale can then be transformed to that on the underlying liability scale using well-established theory. The standard errors (square root of sampling variance) of either or observed in published studies were all highly consistently with those predicted from our approximation theories, which were also confirmed by simulations based on real genotype data.
Analytical expressions for the sampling variance of the estimates of genetic (co)variance from pedigree analyses have been around for over 50 years [17], [26], and statistical power can be derived from these by using the sampling variance and population value of the parameter. However, these expressions are typically for specific structured pedigrees, such as fullsib or halfsib families or twin pairs. There are to our knowledge no simple approximations for general pedigrees, because the inverse of the variance-covariance matrix is required and this is conditional on the actual pedigree structure. The sampling variance of the estimated parameters in a general complex pedigree is usually derived post hoc after the analysis has been performed.
Methods for calculating the power of detecting quantitative trait loci (QTL) in family-based linkage studies have been investigated extensively in the past two decades [16]–[18], [27]. These methods were developed to calculate the power of detecting a QTL but can be generalized for variance components estimation, e.g. estimating the genetic variance using pedigree information. The non-centrality parameter of the test-statistic from a maximum likelihood analysis of variance components is , where L is the likelihood function, and and are the variance covariance matrix under the null and alternative hypotheses respectively [17], [18]. For a specific balanced pedigree design, e.g. fullsibs or nuclear families, the determinant (or inverse) of the V matrix can be computed explicitly, so that the NCP can be calculated without making approximation [16], [17]. For an arbitrary pedigree, can be calculated approximately using Taylor expansions given the variance in family relatedness [18], [27]. Therefore, all these methods explicitly or implicitly require a known pedigree. When the correlations between relatives are small, the first order approximation of the NCP in Rijsdijk et al [18] can be written in our notations as , which is the same as we derived (i.e. , see Equation (4) for ), even though our deviations were based on least squares regression analysis in unrelated samples whereas the derivations in Rijsdijk et al [18] were based on maximum likelihood approach in family data. This approximation is reasonably accurate when correlations between relatives are small for a pedigree-based design, which is not an issue for a population-based design where the genetic relationships between unrelated samples are very small as demonstrated in Yang et al [3]. We show by simulations (Text S1) that for a univariate analysis the LRT statistics calculated based on REML are highly consistent with the chi-squared test-statistics calculated by the Wald test using the sampling variance either observed from the simulations or predicted from our approximation theory (Figure S1).
For a given population, a set of common SNPs and the method of calculating the genetic relationship matrix that we have used here, is a fixed quantity because it depends only on effective population size of the human populations [28]. We used , which was calculated from theory based upon an effective population size of 10,000. Variance in genetic relatedness (and therefore power of detection) can decrease by including many rare SNPs in calculating the GRM because adding more rare SNPs increases the effective population size reflecting recent population expansion. The variance in relatedness can also increase by sampling closer relatives (see below for more discussion) or, for example, by creating a relationship matrix based upon haplotype information. Modifying the GRM can also affect the variance of the off-diagonal elements. For example by applying a weighting of SNPs depending on linkage disequilibrium the variance in the estimates of genetic relationships will decrease so that the sampling variance of the estimate of SNP-based heritability will be increased [29]. Although we derive the theory and show the results based on the SNPs on the whole genome, our approximation theories are also applicable in analyses using a subset of SNPs, e.g. SNPs from a single chromosome. In that case, used in the approximation equations should be either observed empirically from data or derived from theory [28] based on the subset of SNPs.
If there are unknown related samples in the data (cryptic relatedness), will possibly be inflated due to shared environment between close relatives and/or the effects of causal variants in LD with the SNPs but captured by family relatedness, and will be deflated due to the increase of . In fact, the interpretation of changes if there is a substantial proportion of close relatives in the data [30], [31]. This, however, affects GWAS result in a similar way, where the SE of the estimate of a SNP effect from a single SNP analysis (e.g. linear regression for a quantitative trait and logistic regression for a case-control study) will be deflated, causing an inflation of the test-statistics GWAS (often called “genomic inflation” [32]). For the estimation of using all common SNPs, to avoid possible confounding from shared environments and uncaptured causal variants, we suggested in Yang et al. (2010) a stringent threshold, i.e. 0.025, to remove cryptic relatedness from the data so that the estimate of can be compared directly to the results from GWAS in response to the “missing heritability” problem [2]. In practice, observing a much smaller SE of using all common SNPs than that predicted from theory is a caveat suggesting substantial cryptic relatedness remaining in the data.
Using the same experimental design of a sample of conventionally unrelated individuals, the experimenter can increase power by increasing sample size. Fortunately, power increases quadratically with sample size because every new sample is contrasted with all existing samples. The sampling variance of the estimate of the genetic correlation is generally much larger than that of the proportion of variance explained from a univariate analysis, consistent with the theory of the sampling variance of genetic correlations in pedigree designs [33].
Supporting Information
Zdroje
1. HindorffLA, SethupathyP, JunkinsHA, RamosEM, MehtaJP, et al. (2009) Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc Natl Acad Sci USA 106 : 9362–9367.
2. ManolioTA, CollinsFS, CoxNJ, GoldsteinDB, HindorffLA, et al. (2009) Finding the missing heritability of complex diseases. Nature 461 : 747–753.
3. YangJ, BenyaminB, McEvoyBP, GordonS, HendersAK, et al. (2010) Common SNPs explain a large proportion of the heritability for human height. Nat Genet 42 : 565–569.
4. LeeSH, WrayNR, GoddardME, VisscherPM (2011) Estimating missing heritability for disease from genome-wide association studies. Am J Hum Genet 88 : 294–305.
5. DearyIJ, YangJ, DaviesG, HarrisSE, TenesaA, et al. (2012) Genetic contributions to stability and change in intelligence from childhood to old age. Nature 482 : 212–215.
6. LeeSH, YangJ, GoddardME, VisscherPM, WrayNR (2012) Estimation of pleiotropy between complex diseases using single-nucleotide polymorphism-derived genomic relationships and restricted maximum likelihood. Bioinformatics 28 : 2540–2542.
7. LeeSH, RipkeS, NealeBM, FaraoneSV, PurcellSM, et al. (2013) Genetic relationship between five psychiatric disorders estimated from genome-wide SNPs. Nat Genet 45 : 984–994.
8. SoHC, LiM, ShamPC (2011) Uncovering the total heritability explained by all true susceptibility variants in a genome-wide association study. Genet Epidemiol 35 : 447–456.
9. DudbridgeF (2013) Power and predictive accuracy of polygenic risk scores. PLoS Genet 9: e1003348.
10. StahlEA, WegmannD, TrynkaG, Gutierrez-AchuryJ, DoR, et al. (2012) Bayesian inference analyses of the polygenic architecture of rheumatoid arthritis. Nat Genet 44 : 483–489.
11. BenjaminDJ, CesariniD, van der LoosMJ, DawesCT, KoellingerPD, et al. (2012) The genetic architecture of economic and political preferences. Proc Natl Acad Sci U S A 109 : 8026–8031.
12. MeuwissenTH, HayesBJ, GoddardME (2001) Prediction of total genetic value using genome-wide dense marker maps. Genetics 157 : 1819–1829.
13. YangJ, LeeSH, GoddardME, VisscherPM (2011) GCTA: a tool for genome-wide complex trait analysis. Am J Hum Genet 88 : 76–82.
14. PattersonHD, ThompsonR (1971) Recovery of inter-block information when block sizes are unequal. Biometrika 58 : 545–554.
15. Lynch M, Walsh B (1998) Genetics and analysis of quantitative traits: Sunderland, MA: Sinauer Associates.
16. WilliamsJT, BlangeroJ (1999) Power of variance component linkage analysis to detect quantitative trait loci. Ann Hum Genet 63 : 545–563.
17. ShamPC, ChernySS, PurcellS, HewittJK (2000) Power of linkage versus association analysis of quantitative traits, by use of variance-components models, for sibship data. Am J Hum Genet 66 : 1616–1630.
18. RijsdijkFV, HewittJK, ShamPC (2001) Analytic power calculation for QTL linkage analysis of small pedigrees. Eur J Hum Genet 9 : 335–340.
19. ShamPC, PurcellS (2001) Equivalence between Haseman-Elston and variance-components linkage analyses for sib pairs. Am J Hum Genet 68 : 1527–1532.
20. VisscherPM, HopperJL (2001) Power of regression and maximum likelihood methods to map QTL from sib-pair and DZ twin data. Ann Hum Genet 65 : 583–601.
21. VinkhuyzenAA, WrayNR, YangJ, GoddardME, VisscherPM (2013) Estimation and Partitioning of Heritability in Human Populations Using Whole Genome Analysis Methods. Annual Review of Genetics 47.
22. YangJ, ManolioTA, PasqualeLR, BoerwinkleE, CaporasoN, et al. (2011) Genome partitioning of genetic variation for complex traits using common SNPs. Nat Genet 43 : 519–525.
23. ReeveECR (1955) The variance of the genetic correlation coeffi - cient. Biometrics 11 : 357–374.
24. RobertsonA (1959) The sampling variance of the genetic correlation coefficient. Biometrics 15 : 469–485.
25. KootsKR, GibsonJP (1996) Realized sampling variances of estimates of genetic parameters and the difference between genetic and phenotypic correlations. Genetics 143 : 1409–1416.
26. Falconer DS, Mackay TFC (1996) Introduction to quantitative genetics: England: Longman.
27. ChenWM, AbecasisGR (2006) Estimating the power of variance component linkage analysis in large pedigrees. Genet Epidemiol 30 : 471–484.
28. GoddardME (2009) Genomic selection: prediction of accuracy and maximisation of long term. Genetica 136 : 245–257.
29. SpeedD, HemaniG, JohnsonMR, BaldingDJ (2012) Improved heritability estimation from genome-wide SNPs. Am J Hum Genet 91 : 1011–1021.
30. VisscherPM, YangJ, GoddardME (2010) A Commentary on ‘Common SNPs Explain a Large Proportion of the Heritability for Human Height’ by Yang et al. (2010). Twin Res Hum Genet 13 : 517–524.
31. WrayNR, YangJ, HayesBJ, PriceAL, GoddardME, et al. (2013) Author reply to A commentary on Pitfalls of predicting complex traits from SNPs. Nat Rev Genet 14 : 894.
32. DevlinB, RoederK (1999) Genomic control for association studies. Biometrics 55 : 997–1004.
33. VisscherPM (1998) On the sampling variance of intraclass correlations and genetic correlations. Genetics 149 : 1605–1614.
34. LeeSH, HaroldD, NyholtDR, GoddardME, ZondervanKT, et al. (2013) Estimation and partitioning of polygenic variation captured by common SNPs for Alzheimer's disease, multiple sclerosis and endometriosis. Hum Mol Genet 22 : 832–841.
Štítky
Genetika Reprodukční medicínaČlánek vyšel v časopise
PLOS Genetics
2014 Číslo 4
Nejčtenější v tomto čísle
- The Sequence-Specific Transcription Factor c-Jun Targets Cockayne Syndrome Protein B to Regulate Transcription and Chromatin Structure
- The Mechanism of Gene Targeting in Human Somatic Cells
- Genetic Predisposition to In Situ and Invasive Lobular Carcinoma of the Breast
- Widespread Use of Non-productive Alternative Splice Sites in
Zvyšte si kvalifikaci online z pohodlí domova
Současné možnosti léčby obezity
nový kurzVšechny kurzy

















