Demography and the Age of Rare Variants
In this paper we describe a method for estimating the age of rare genetic variants. These ages are highly informative about the extent and dates of connections between populations. Variants in closely related populations generally arose more recently than variants of the same frequency in more diverged populations. Therefore, comparing the ages of variants shared across different populations allows us to infer the dates of demographic events like population splits and bottlenecks. We also see that rare functional variants shared within populations tend to have more recent origins than nonfunctional variants, which is consistent with the effects of natural selection.
Published in the journal:
. PLoS Genet 10(8): e32767. doi:10.1371/journal.pgen.1004528
Category:
Research Article
doi:
https://doi.org/10.1371/journal.pgen.1004528
Summary
In this paper we describe a method for estimating the age of rare genetic variants. These ages are highly informative about the extent and dates of connections between populations. Variants in closely related populations generally arose more recently than variants of the same frequency in more diverged populations. Therefore, comparing the ages of variants shared across different populations allows us to infer the dates of demographic events like population splits and bottlenecks. We also see that rare functional variants shared within populations tend to have more recent origins than nonfunctional variants, which is consistent with the effects of natural selection.
Introduction
The recent availability of large numbers of fully sequenced human genomes has allowed, for the first time, detailed investigation of rare genetic variants. These are highly differentiated between populations [1], [2], may make an important contribution to genetic susceptibility to disease [3]–[7], and provide information about both demographic history, and fine-scale population structure [8], [9]. While patterns of rare variant sharing are informative in themselves, knowing the age of the variants allows us to observe changes in structure over time, and thus to infer the dates of demographic events.
Rare variants are typically more recent than common variants and in fact, the age of a variant can be estimated directly from its frequency [10]–[12]. However there are two problems with this approach. First, using only the frequency information means that we cannot distinguish differences between the ages of variants which are at the same frequency which, as we demonstrate here, can be both large and important. Second, in order to use this approach, we have to know the demographic history of the populations involved. In this article, we describe an alternative approach which uses the fact that the lengths of shared haplotypes around variants are informative about their ages [13]–[15].
Specifically, we estimate the time to the most recent common ancestor (TMRCA) for haplotypes, which are regions where two chromosomes are each other's closest relative in a sample. More precisely, haplotypes are genomic regions where two chromosomes are each other's unique closest relative within at least some of the region and where their TMRCA is constant. To find these regions, we look for variants which occur exactly twice in the sample ( variants, or doubletons). We then use the length of, and number of mutations on, these haplotype to infer their ages, and therefore a lower bound for the age of the variants they carry. Every variant identifies an haplotype, but we do not detect all haplotypes because not all of them carry mutations. This approach is highly scalable and finds shared haplotypes directly from genotype data, which avoids the need for statistical phasing. We apply this method to the 1000 Genomes phase 1 dataset [16], to quantify the distribution of the ages of variants shared within and between populations, and between variants in different functional classes. We demonstrate dramatic differences between the ages of variants shared across different populations, and observe the effects of both demography and selective constraint.
Results
We first give a brief outline of our approach (Figures 1, S1, Methods). Given a sample of individual genotypes, we find all variants. That is, variants which have exactly two copies (in different individuals) in the sample. This tells us that, in the absence of repeat mutations and assuming that the variant is derived, those individuals must share an haplotype at that position. We then scan left and right along the genome, until we reach a point where the two individuals have inconsistent homozygote genotypes (0 and 2, Figure 1A), which gives us an (over-) estimate of the distance to the first recombination breaking the haplotype.
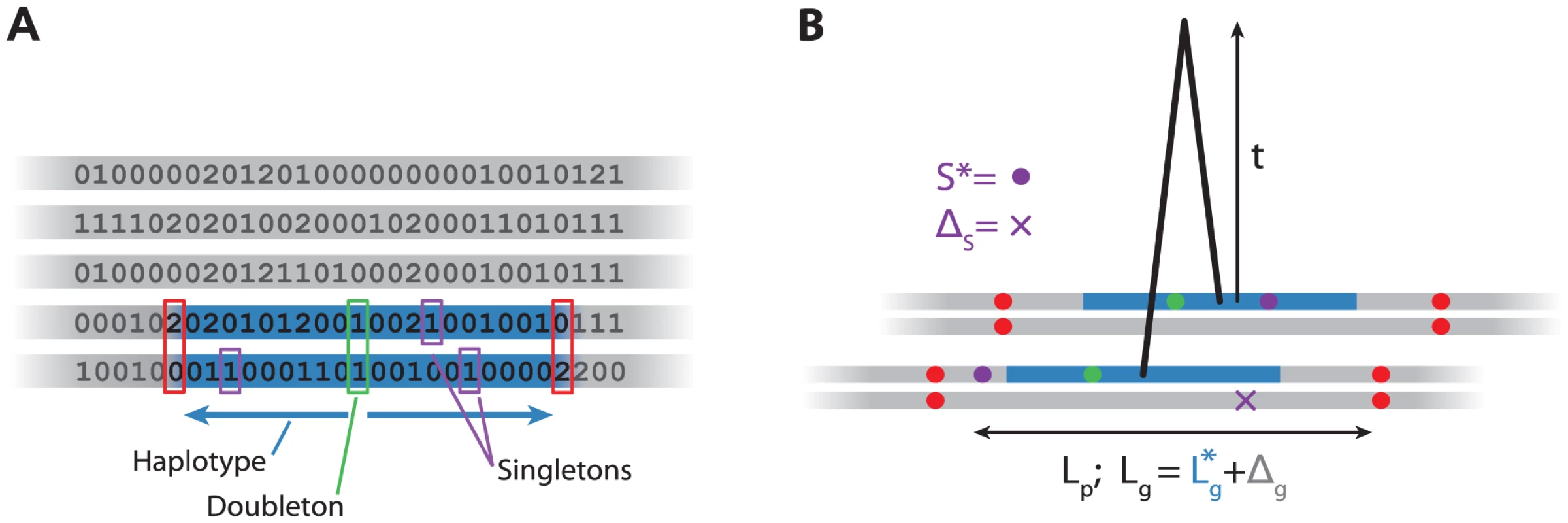
Using both the genetic and physical lengths of the region, and the number of singletons, we compute an approximate likelihood for the age of the haplotype (Figure 1B). We use the data to estimate error terms to take into account the fact that the algorithm described above does not find the shared haplotypes precisely. Then, for each haplotype, we find the maximum likelihood estimate (MLE) of the age of each haplotype. We investigate the distribution of these MLEs for different classes of variants, for example those shared within or between specific populations.
Simulation results
To test our approach, we ran whole genome simulations for a sample of 100 diploid individuals with MaCS [17], using the combined HapMap 2 recombination maps [18], and a mutation rate () of per-base per-generation, assuming a constant effective population size () of 14,000; chosen to reflect parameters relevant to human genetic variation. We investigated both our power to detect the haplotypes and how accurately we could estimate the distribution of ages (Figure 2). We detected around 26% of all haplotypes. Unsurprisingly, we have more power to detect very long haplotypes, but we detected many small haplotypes as well: 19% of our total had true genetic length less than than 0.1 cM. Having imperfect power to detect variants does not have a large effect on our power to detect haplotypes since most detected haplotypes carry more than one variant. We have higher power for more recent haplotypes because they are longer but, at least for a population of constant size, this effect is cancelled to some extent for older haplotypes because the branches above them tend to be longer and therefore more likely to carry mutations.
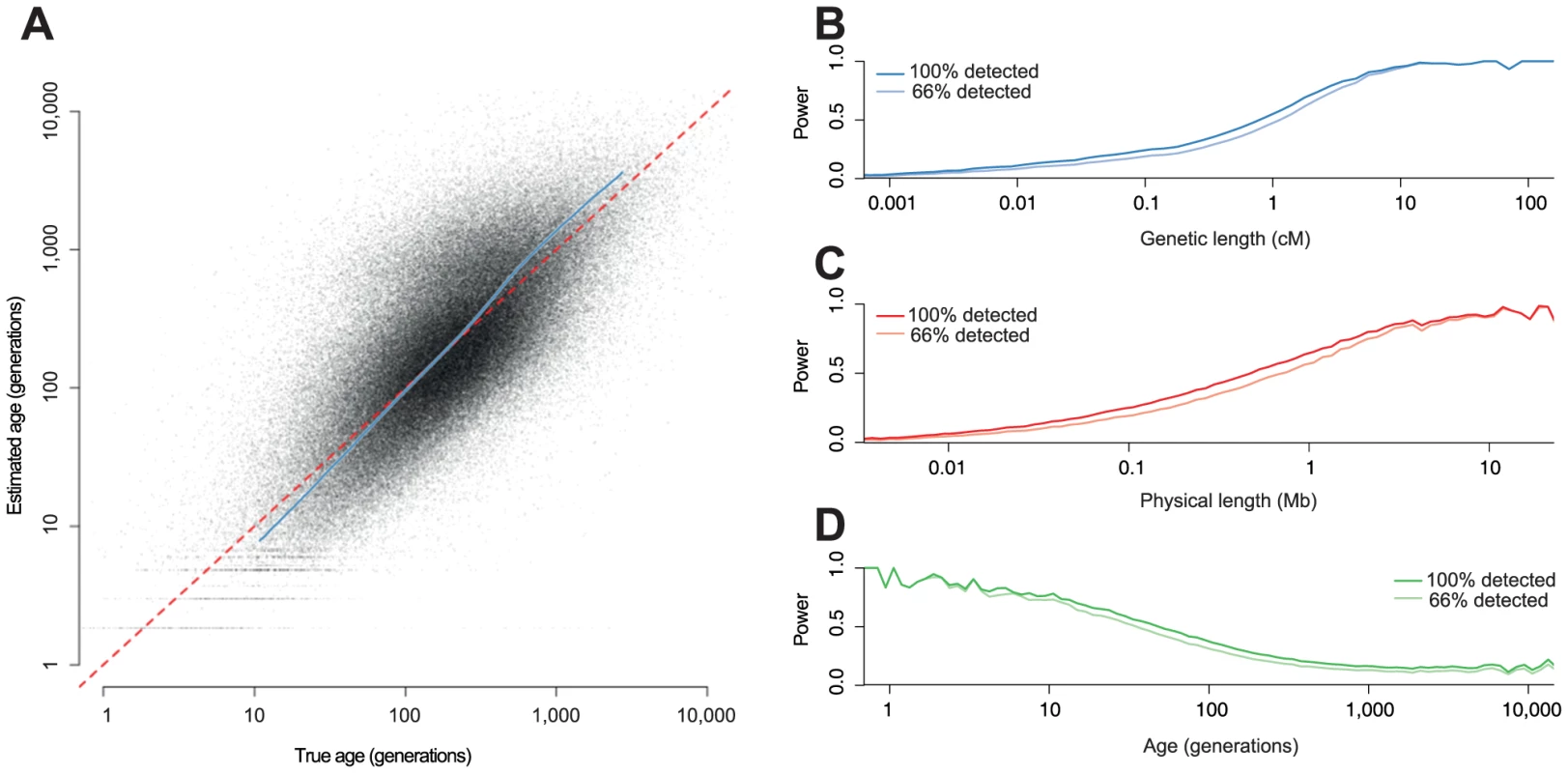
There is high uncertainly in the age of any individual haplotype (Figure 2A). However, we can compute well-calibrated confidence intervals (Figure S2). In this example, the median MLE of the age of the detected haplotypes is 179 generations and the true median is 192 generations. The median width of the 95% confidence interval is 730 generations. Information about the ages comes mainly from the genetic length, and the principal advantage of the singleton information is for very old haplotypes where the length-based estimator is otherwise biased (Figure S3).
In addition, we ran simulations to check that the model was robust to more complicated demographic scenarios including splits, bottlenecks and expansions, as well as mis-specification of (Figure S4). We also investigated the effect that these scenarios had on the distribution of the ages of the haplotypes, demonstrating that we could detect the signatures of demographic events. For example, population bottlenecks lead to a high density of haplotypes during the bottleneck and, following a population split haplotypes shared between populations have median age roughly equal to the split time (Figure S5).
1000 Genomes data
We applied our estimator to the phase 1 data release of the 1000 Genomes Project [16], which consists of whole-genome variant calls for 1,092 individuals drawn from 14 populations (Table 1). We used two of the 1000 Genomes callsets; one made from sequence data, and one made using a dense genotyping array. Restricting our analysis to the autosomes, we extracted variants from the sequence data callset, and then detected haplotype lengths around them (that is, the distances to incompatible homozygotes), using only the array data, to minimise the effect of genotyping errors. We then counted variants on these haplotypes from the sequence data callset. From 4,066,530 variants we detected 1,893,391 haplotypes, with median genetic and physical lengths of 0.7 cM and 600 kb respectively. The median number of singletons spanned by each haplotype was 3. Of the 1.9 million haplotypes, 0.7 million were shared within populations and 1.5 million were shared within continents. Sharing of variants largely reflects expected patterns of relatedness on a population level, and also reveals substructure in some populations, notably GBR (Figure S6).
We used the combined recombination rate map from HapMap 2 to determine genetic lengths, and assumed a mutation rate of per-base per-generation (reflecting a true mutation rate of multiplied by a power of to detect singletons [16], [19]). We then computed MLEs for the ages of all the haplotypes shared between every pair of populations (Figures 3, S7, Tables S1–S5). By considering the distribution of the distance between inconsistent homozygous SNPs, we estimated that on most chromosomes the median overestimate in haplotype length due to the sparsity of informative SNPs was 0.1–0.15 cM (but more on chromosomes 1, 9 and 15). We also estimated that (estimated from singletons) was around and per-base for African and Non-African populations respectively (Table S6).
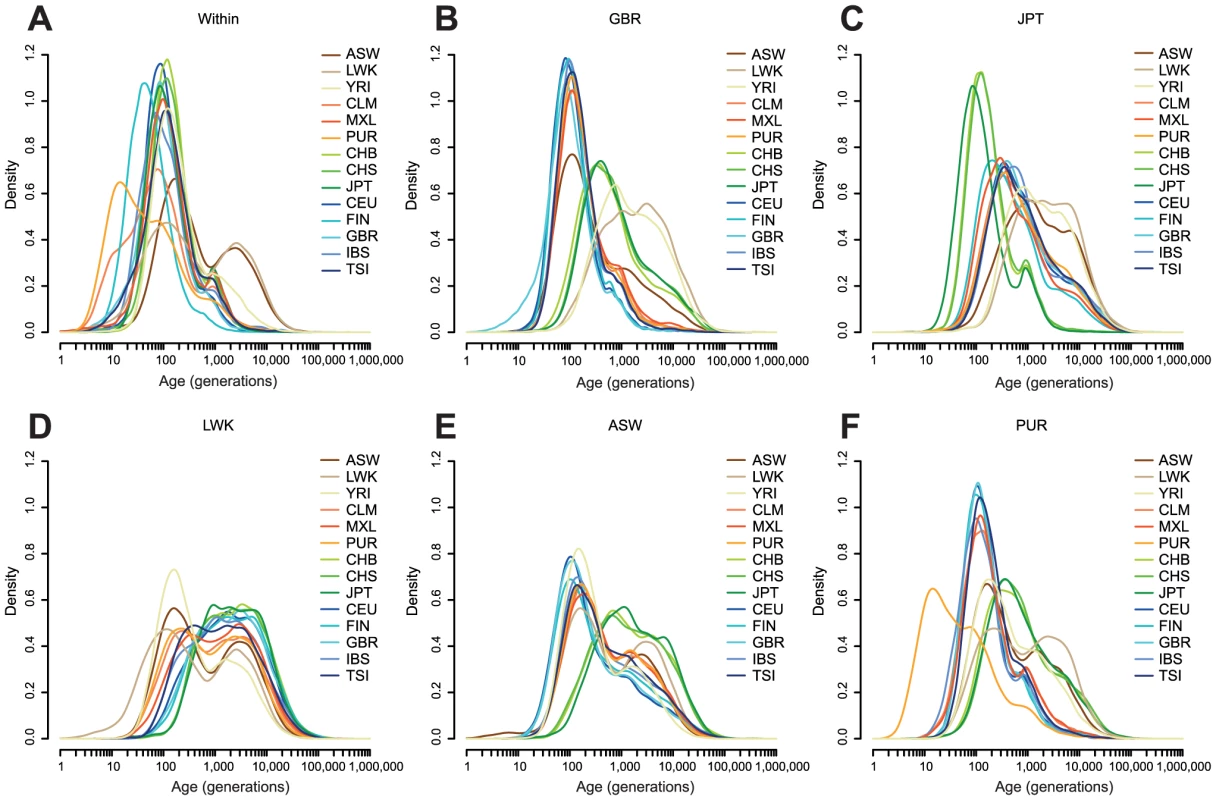
For haplotypes shared within populations (Figure 3A), the MLEs of haplotypes within most European and Asian populations are clustered around 100 generations ago. For example, the median age of GBR-GBR haplotypes is 90 generations. PUR and, to a lesser extent, CLM have many very recent haplotypes (peaking around 11 generations ago), consistent with a historical bottleneck in these populations 300–350 years ago. FIN haplotypes peak around 14 generations (400–450 years) ago. African populations have many recent haplotypes but also a much longer tail than the other populations, with ancestry apparently extending back for thousands of generations. For example the median age of LWK-LWK haplotypes is 320 generations, but the 95% quantile is 8,500 generations.
Between-population sharing is largely consistent with the historical relationships among populations (Figure 3B–D). Within continents, sharing within Asia or Europe has a median of 50–160 generations, depending on the populations, and sharing within Africa 170–340 generations. Sharing between continents is much older, with median Asian-European sharing 320–670 generations old, and Asian-African sharing rather older, with a median around 2,300 generations ago for LWK and 1,700 generations ago for YRI. The age of European-African sharing varies between populations, from 1,000 to 2,000 generations ago, but is more recent than Asian-African sharing, perhaps suggesting greater subsequent migration between these continents. We discuss these figures in the context of split times and migrations in the Discussion.
Admixed populations have age distributions that are combinations of the distributions of the admixing populations (Figure 3E–F). Even in these populations we can see signs of more subtle history. For example, GBR-CLM haplotypes have an age distribution which looks more like GBR-TSI or GBR-IBS than GBR-CEU, presumably representing the fact that the major contribution to European admixture in the Americas is from southern Europe (Figure S8).
We also looked at the distribution of the ages of variants broken down by functional annotation (Figure 4, Methods). We found that for variants shared within a single population, loss-of-function (LOF) variants are younger than coding variants, which are younger than functional noncoding variants, and all annotated variants are younger than unannotated variants. The median ages of these variants are 58, 83, 112 and 125 generations for LOF, coding, functional noncoding and unannotated variants respectively. This is presumably because purifying selection against damaging mutations means that functional variants are less likely to become old (though positive selection for beneficial mutations would have the same effect). This effect has previously been both predicted and observed [20],[21]. However, it is not strictly true for variants shared between different populations and, in fact, the effect is partially reversed (median ages are 176, 205, 186 and 195 generations for LOF, coding, functional noncoding and unannotated variants). One possible explanation is that functional variants surviving long enough to be shared between populations are selectively neutral or recessive and thus unaffected by selection at low frequency. This suggests that studies looking for disease-causing rare variants should concentrate on variants private to a single population, since variants shared across populations are unlikely to have large phenotypic effects.
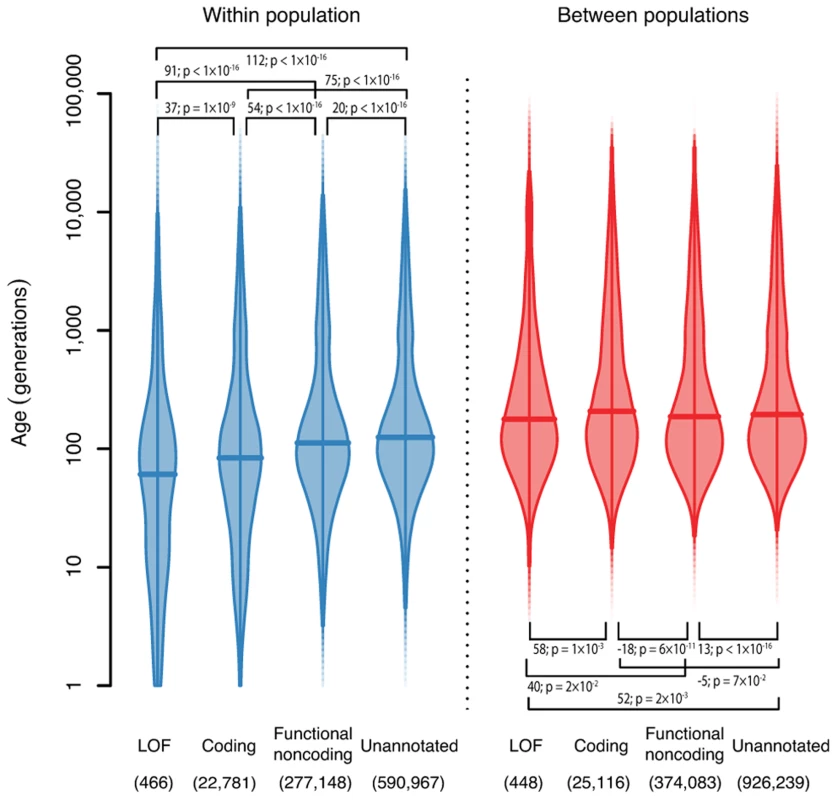
Robustness
This analysis requires us to estimate several parameters, and in this section, we investigate how robust it is to varying them.
The parameter is related to the probability of discovering haplotypes. We know that . implies that the probability that we discover a haplotype is independent of its length while implies that this probability increases linearly with length. We chose based on simulations, but it may be the case that this is not optimal for real data. To test how much of an impact this might have, we re-ran the analysis of the 1000 Genomes data using and . Larger values of increase our age estimates. For example, the median CEU-CHB age is 403, 481 and 560 generations using , 1.5 and 2 respectively. Overall, setting increases the median age estimates by between 6 and 30%, depending on population, with more recent ages more sensitive to .
The parameters and are the shape and rate of the (gamma) distribution of the overestimate of haplotype lengths (Methods). We estimated these parameters separately from the array data for each chromosome (Table S6). We noticed that chromosomes 1, 5 and 9 had estimated parameters that implied a greater overestimate (larger , smaller ), presumably due to the density of markers on the array for those chromosomes. In addition, these chromosomes had older estimated haplotype ages, for example we estimated that the median age of haplotypes on chromosome 1 was 16% higher than the median age of haplotypes on chromosome 2, suggesting that our error model is not fully robust to variation in marker density.
Discussion
We described an approach to estimate the age of haplotypes, without making any prior assumptions about population structure or history. Though the age of any individual haplotype is uncertain, major features of the distribution of haplotype ages are detected, demonstrating qualitative differences between populations that are almost certainly due to past demographic events. The next important question is to what extent we can use these distributions as quantitative estimates of the ages of demographic events.
Consider the split between European and East Asian populations. Model based estimates of this split time have ranged from 14 to 40 thousand years ago (kya) [22]–[24]. However these are likely to be too low because they assumed a mutation rate, , of per-base per-generation, now thought to be an overestimate [19] and so a more reasonable range of estimates might be 22–80 kya. The nonparametric PSMC approach [25] estimated a split time of around 22 kya (if a lower mutation rate of is used, 11 kya with the higher rate), and a similar method, MSMC, estimates a split time of 20–40 kya [26] (Figure 5A). Simulations suggest that, under a clean split model, the median of our estimated ages is close to or slightly below the split time, at least for recent splits (less than 1,000 generations; Figures S5 and S9). Comparing CEU to each of CHB, CHS and JPT, taking the median of our haplotype ages, and assuming a generation time of 30 years [27], would imply split times of 14, 17 and 18 kya respectively. Other European populations give different estimates, but mostly between 15 and 20 kya.
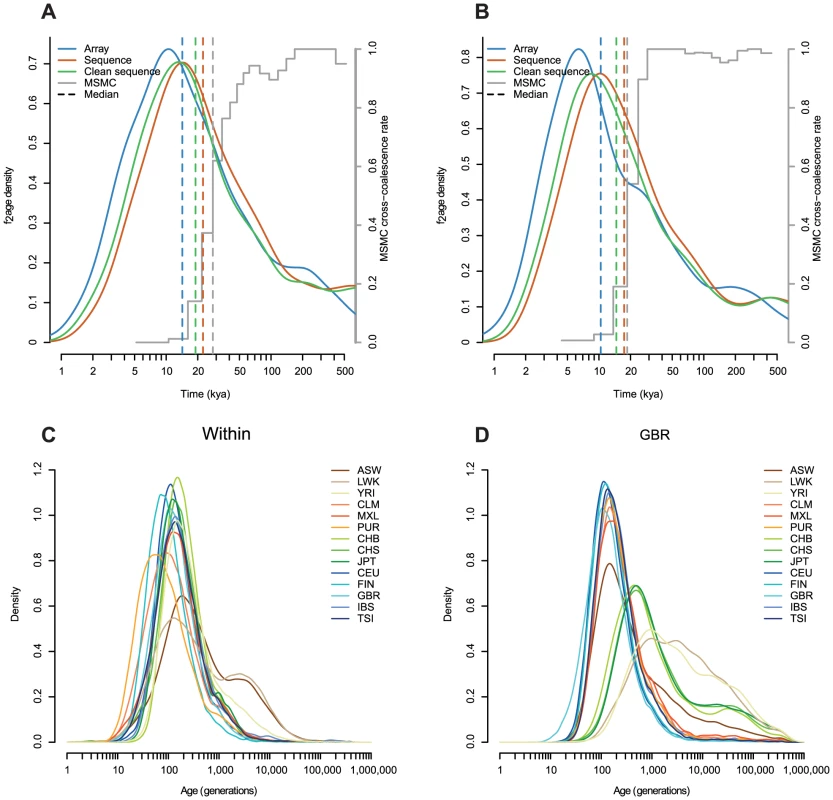
Similarly, when we looked at variants shared between East Asia and America (CHB-MXL, but restricting to regions homozygous for Native American ancestry in MXL; Methods), we found that the median age was around 10 kya, substantially more recent than the 20 kya split time estimated using MSMC [26] (Figure 5B). This seems low, given geological evidence that the Bering land bridge was submerged by 11–13 kya, although a seasonal or maritime route likely remained open after that time [28]–[30].
Our dates are all around or below the low end of published estimates, even after we take into account the fact that the median might be lower than the split time (we estimate about 11% lower for a 500-generation old split; Figure S5D). There are several non-exclusive explanations for this observation. First, post-split gene flow could explain the discrepancy. As we have greater power to detect haplotypes if they are more recent, when the split is not clean many of the haplotypes we observe will derive from the post-split gene flow rather than from before the initial split (Figure S9B). In this scenario, we would be detecting the most recent haplotypes, and our dates would be closer to the most recent date of contact, rather than the initial split date.
An alternative explanation might be systematic errors in our estimates. As we described in the Results, the approach is sensitive to the estimated parameters , and . At the extreme, increasing from 1.5 to its maximum value of 2 would increase the median age of CEU-CHB haplotypes from 14 kya to 17 kya. To investigate sensitivity to and , we repeated the analysis, but using sequence data rather than array data to find the length of the haplotypes (Figure 5). We note that when we estimated and using sequence data they vary very little across chromosomes (Table S6). The ages estimated using sequence data were older than those estimated using array data (median age of CEU-CHB haplotypes 23 kya, Figure 5A–B). We might expect that sequence data, being denser than array data, would find haplotypes more accurately. However we would also expect that genotype errors, more common in sequence than array data, would make all haplotypes look older, by incorrectly breaking haplotypes. Removing indels and low complexity regions (LCRs; Methods) thought to be enriched for genotyping errors from the sequence data reduced the difference (median CEU-CHB age of 19 kya), suggesting that around half the increase in age is driven by errors. Further, the haplotype ages estimated from sequence data do not contain the very young (long) haplotypes within CLM, FIN and PUR, which we independently believe to be correct (Figure 5C), and also contain a long tail of extremely old haplotypes which seems unlikely (Figure 5D).
Another source of systematic errors could be the use of incorrect mutation or recombination rates. There is considerable uncertainty about the mutation rate in humans, but our approach is relatively insensitive to this, so if the true rate is higher than per-base per-generation then mutational clock based methods which scale linearly with mutation rate will overestimate the ages of events, thus reducing the discrepancy.
On the other hand, our approach might be sensitive to errors in the recombination map. We tested this by running simulations with a different genetic map to the HapMap map that we used to determine genetic length. We tested a population-based African American map [31], a map derived from an Icelandic pedigree [32] and a chimpanzee map from a small population [33], but none of these made a substantial difference to the results and we conclude that the length of the haplotypes we investigate is sufficiently large that they are robust to the uncertainty in the recombination map (Figure S10).
Finally, systematic errors might occur due to homoplasy (where the same mutation occurs independently on two different lineages). While this rate is expected to be low, it may be locally high in some parts of the genome, for example in CpG islands which have an order of magnitude higher mutation rate than the genomic background. If such false positives do occur, they would appear as very short haplotypes that we would infer to be very old, so they cannot explain our systematically lower ages. On the other hand, it is likely that some of the very old haplotypes we see are, in fact, due to repeat mutations and, in particular, this might explain some of the very old haplotypes discovered with sequence data.
However, while systematic biases in our estimates might explain some of the difference between our estimated ages and independent split time estimates, they are unlikely to explain the observation that the age distributions vary greatly between different pairs of populations. This strongly suggests that there is variation in the extent of gene flow. For example, Asian-FIN sharing seems to be more recent than other Asian-European sharing, suggesting relatively recent contact between East Asian and Finnish populations, compared to other European populations. It seems likely that worldwide demographic history is sufficiently complicated that trying to estimate a single Asian-European (or African-Non African) split time is futile, and that a complex model of many splits, migrations and admixtures is required to explain the relationship between different populations.
Ultimately, we would like to be able to make explicit estimates of parameters like historical effective population size, and the dates of demographic events. Though the approach we describe here is limited in in this respect, there is a clear path to extend it to do so. We could first use a similar approach to estimate the ages of variants at frequency three and higher. Then, treating the estimates of haplotype ages as estimates of coalescent times, we could use the empirical distribution of coalescent times to estimate population sizes and cross-population migration rates as a function of time. Another improvement would be to use information from the full likelihood surface for each haplotype, rather than just the point estimate of the age as we do here. Since, for large samples, we would have good estimates of recent coalescent rates, we expect that this approach would be very accurate at inferring recent history, making it a complementary approach to sequential Markovian coalescent based methods which are typically accurate in the ancient past, but less so for very recent history.
Methods
Definitions
Suppose we have a sample of size of genotypes from a single genetic region. Define an variant to be one which occurs exactly twice in the sample in different individuals. That is, either two individuals have genotype 1 and all the others have genotype 0, or two individuals have genotype 1 and the others have genotype 2. We assume that the minor allele is the derived allele. Under the neutral coalescent, for a sample of chromosomes, an minor allele will be the derived allele with probability for large so this is a reasonable assumption for large samples.
Define an haplotype shared between chromosomes and to be a region satisfying the following two conditions: 1) The time to the most recent common ancestor (TMRCA) of and does not change over the region. 2) At one or more sites in the region, and coalesce with each other before either of them coalesce with any other chromosome. In other words, they are unique genealogical nearest neighbours (Figure S1). We call the TMRCA of and the age of the haplotype. Additionally, we say that individuals and () share an haplotype if is one of 's two chromosomes and is one of 's two chromosomes.
The problem we solve is to find the haplotypes and then estimate their ages. Since each variant must lie in an haplotype, the variants provide a simple way of detecting the haplotypes. We use the algorithm described in the main text to find regions which should be larger than the haplotypes. The next problem is to determine the likelihood of the age. We describe our approximate likelihood below but first, as an example, we describe exact inference in the absence of confounding factors.
Exact case
Suppose we knew the exact genetic and physical lengths of an haplotype and the number of singletons it carries. Call these quantities and . Let the age of this haplotype be generations, or in coalescent time (). Then, for a randomly chosen haplotype (but not a haplotype at a randomly chosen position, discussed in the next section), has an exponential distribution with parameter and has a Poisson distribution with parameter where and is the per-base per-generation mutation rate. Therefore (ignoring terms that do not depend on ), the log-likelihood of given and is
and the maximum likelihood estimator of is therefore
Approximate likelihood for genetic length
There are two corrections to the likelihood for genetic length. The first relates to the ascertainment process of the haplotypes, and the second to the overestimate in the length due to the way we detect the endpoints.
The ascertainment problem is as follows. Suppose we pick a haplotype at random, then its length is exponentially distributed (i.e. gamma with shape parameter 1). However, if we pick a point on the sequence at random then the distribution of the length of the haplotype in which it falls is gamma distributed with shape parameter 2. This is an example of the “inspection paradox” and it is because in the second case, we are sampling haplotypes effectively weighted by their length. In our case, we detect haplotypes if they contain one or more variants. Therefore the probability that we find a haplotype is increasing with its physical length (because longer haplotypes are more likely to carry variants), but sub-linearly. The probability also increases with genetic length, but in a complex way that depends on the variation of recombination and mutation rate along the genome, the age of the haplotype and the demographic history of the population. For example, in a constant sized population, older haplotypes are likely to have longer branches above them, and therefore to have more variants, but in an expanding population the opposite may be true. Rather than trying to take all of these effects into account, we made the simplifying assumption that we could model the genetic length as a gamma distribution with shape parameter where and rate . Simulations suggested that around 1.5 was optimal (Figure S11), and we used this value throughout.
The second correction involves the overestimate of genetic length. We tried to detect the ends of the haplotype by looking for inconsistent homozygote genotypes, but of course in practice, after the end of the haplotype, there will be some distance before reaching such a site. This (genetic) distance is the amount by which we overestimate the length of the haplotype. We estimate the distribution of for a given sample by sampling pairs of genotype vectors, then sampling sites at random and computing the sum of genetic distance to the first inconsistent homozygote site on either side. We then fit a gamma distribution with (shape, rate) parameters to this distribution, for each chromosome. The likelihood of is given by the convolution density of and ,
where is the density of a gamma distribution with (shape, rate) parameters . This integral, and therefore the loglikelihood can be expressed in terms of the confluent hypergeometric function (ignoring terms that do not depend on ),Where, recall, we assume . Note that if we replace with , and drop constant terms, then we get an expression for the likelihood of that does not depend on , so our estimate of time in generations does not depend on .
Finally, note that the rate at which recombination events occur on the branch connecting the two shared haplotypes is . We assume that the first such event marks the end of the haplotype. However, there is a non-zero probability that a recombination event occurring on this branch does not change the MRCA of and . Simulations suggest that for large numbers of chromosomes, this probability is extremely small (Figure S12) and so we assume it is 0. In practice, for small samples, this might be a non-negligible effect.
Approximate likelihood for singleton count
Recall that the physical length of the shared haplotype is bases. We assume that we can find this exactly. Then assuming a constant mutation rate per base per generation, the sum of the number of singletons on the shared haplotypes, has a Poisson distribution with parameter , where .
Now consider the distribution of singletons on the unshared haplotypes. To approximate this distribution, we make the following three assumptions: 1) There is no recombination on the unshared haplotypes over the region. 2) No other lineage coalesces with the shared haplotype before it is broken. 3) The distribution of the time to first coalescence of the unshared haplotypes is exponential with parameter (Recall that is the number of sampled individuals). In fact the true distribution is a mixture of exponentials but the approximation at least matches the correct mean, [34]. The variance is too small because of the first assumption, however.
Consider one of the unshared haplotypes. Conditional on the time () at which it first coalesces with any other haplotype, the number of singleton mutations it carries is Poisson with parameter and so, using the assumptions above, the unconditional distribution is geometric (on ) with parameter . Therefore the distribution of the number of mutations on both unshared haplotypes, , is the sum of two geometric distributions which is negative binomial with parameters . The density of the total number of singletons, is the convolution of these two densities
where is the density of a Poisson distribution with parameter and is the density of a negative binomial distribution with parameters . As with the genetic length, we can write this in terms of , the haplotype age in generations,In practice we assume is known and estimate separately for each individual, for each chromosome, by counting the number of singletons, multiplying by the number of chromosomes in the sample, and dividing by the chromosome length. Then for each pair, we use use the average of these values in Equation 5. A more accurate approach would be to compute the likelihood as a double convolution over the distribution of both haplotypes with different values for . An extension would be to estimate separately for different regions of the genome.
Approximate full likelihood
We can now write the approximate log-likelihood for as the sum of Equation 3 and the log of Equation 5, assuming that the recombination process is independent of the mutational process,
We maximise it numerically with respect to in order to find the maximum likelihood estimate (MLE). It is possible for this likelihood to be bimodal, in which case we might find a local but not global optimum. However, this seems to be rare.
1000 Genomes data
The 1000 Genomes data was obtained from ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/. The phase 1 release sequence data is in phase1/analysis_results/integrated_call_sets, and the array data is in phase1/analysis_results/supporting/omni_haplotypes. In order to generate the “clean” sequence data, we removed any sites that fell in the list of low complexity regions found in technical/working/20140224_low_complexity_regions/hs37d5-LCRs.txt. Functional annotations are in phase1/analysis_results/functional_annotation. Detailed explanations of the annotations can be found there, but briefly the classifications are as follows:
-
Loss-of-function: Includes premature stop codons, and essential splice site disruptions.
-
Coding: Variants in coding regions.
-
Functional noncoding: Including variants in noncoding RNAs, promoters, enhancers and transcription factor binding sites.
-
Unannotated: Any variant not included in any of the above categories.
We included haplotypes in more than one of these categories if they contained multiple variants.
Code
All the code we used to run simulations and analyse the 1000 Genomes data is available from www.github.com/mathii/f2.
Supporting Information
Zdroje
1. BustamanteCD, BurchardEG, De la VegaFM (2011) Genomics for the world. Nature 475 : 163–165.
2. NelsonMR, WegmannD, EhmMG, KessnerD, St JeanP, et al. (2012) An abundance of rare functional variants in 202 drug target genes sequenced in 14,002 people. Science 337 : 100–104.
3. NejentsevS, WalkerN, RichesD, EgholmM, ToddJA (2009) Rare variants of IFIH1, a gene implicated in antiviral responses, protect against type 1 diabetes. Science 324 : 387–389.
4. JohansenCT, WangJ, LanktreeMB, CaoH, McIntyreAD, et al. (2010) Excess of rare variants in genes identified by genome-wide association study of hypertriglyceridemia. Nature Genetics 42 : 684–687.
5. McClellanJ, KingMC (2010) Genetic Heterogeneity in Human Disease. Cell 141 : 210–217.
6. RivasMA, BeaudoinM, GardetA, StevensC, SharmaY, et al. (2011) Deep resequencing of GWAS loci identifies independent rare variants associated with inflammatory bowel disease. Nature Genetics 43 : 1066–1073.
7. BeaudoinM, GoyetteP, BoucherG, LoKS, RivasMA, et al. (2013) Deep resequencing of GWAS loci identifies rare variants in CARD9, IL23R and RNF186 that are associated with ulcerative colitis. PLoS Genetics 9: e1003723.
8. GravelS, HennBM, GutenkunstRN (2011) Demographic history and rare allele sharing among human populations. Proceedings of the National Academy of Sciences 108 : 11983–11988.
9. MathiesonI, McVeanG (2012) Differential confounding of rare and common variants in spatially structured populations. Nature Genetics 44 : 243–246.
10. KimuraM, OhtaT (1973) The age of a neutral mutant persisting in a finite population. Genetics 75 : 199–212.
11. GriffithsRC, TavaréS (1998) The age of a mutation in a general coalescent tree. Communications in Statistics Stochastic Models 14 : 273–295.
12. FuW, O'ConnorTD, JunG, KangHM, AbecasisG, et al. (2013) Analysis of 6,515 exomes reveals the recent origin of most human protein-coding variants. Nature 493 : 216–220.
13. PalamaraPF, LenczT, DarvasiA, Pe'erI (2012) Length distributions of identity by descent reveal fine-scale demographic history. American Journal of Human Genetics 91 : 809–822.
14. RalphP, CoopG (2013) The geography of recent genetic ancestry across Europe. PLoS Biology 11: e1001555.
15. HarrisK, NielsenR (2013) Inferring demographic history from a spectrum of shared haplotype lengths. PLoS Genetics 9: e1003521.
16. Genomes Project Consortium (2012) An integrated map of genetic variation from 1,092 human genomes. Nature 491 : 56–65.
17. ChenGK, MarjoramP, WallJD (2009) Fast and flexible simulation of DNA sequence data. Genome Research 19 : 136–142.
18. International HapMapConsortium (2007) A second generation human haplotype map of over 3.1 million SNPs. Nature 449 : 851–861.
19. ScallyA, DurbinR (2012) Revising the human mutation rate: implications for understanding human evolution. Nature Reviews Genetics 13 : 745–753.
20. MaruyamaT (1974) The age of a rare mutant gene in a large population. American Journal of Human Genetics 26 : 669–673.
21. KiezunA, PulitSL, FrancioliLC, van DijkF, SwertzM, et al. (2013) Deleterious alleles in the human genome are on average younger than neutral alleles of the same frequency. PLoS Genetics 9: e1003301.
22. KeinanA, MullikinJC, PattersonN, ReichD (2007) Measurement of the human allele frequency spectrum demonstrates greater genetic drift in East Asians than in Europeans. Nature Genetics 39 : 1251–1255.
23. GutenkunstRN, HernandezRD, WilliamsonSH (2009) Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data. PLoS Genetics 5: e1000695.
24. GronauI, HubiszMJ, GulkoB, DankoCG, SiepelA (2011) Bayesian inference of ancient human demography from individual genome sequences. Nature Genetics 43 : 1031–1034.
25. LiH, DurbinR (2011) Inference of human population history from individual whole-genome sequences. Nature 475 : 493–496.
26. Schiffels S, Durbin R (2014) Inferring human population size and separation history from multiple genome sequences. Nature Genetics: In press.
27. FennerJN (2005) Cross-cultural estimation of the human generation interval for use in genetics-based population divergence studies. American Journal of Physical Anthropology 128 : 415–423.
28. Brigham-Grette J, Anderson PM, Lozhkin AV, Glushkova OV (2004) Paleoenvironmental conditions in western Beringia before and during the Last Glacial Maximum. In: Madsen DB, editor, Entering America. Northeast Asia and Beringia Before the Last Glacial Maximum., University of Utah Press. pp. 29–61.
29. KeigwinLD, DonnellyJP, CookMS, DriscollNW, Brigham-GretteJ (2006) Rapid sea-level rise and Holocene climate in the Chukchi Sea. Geology 34 : 861–864.
30. Meltzer DJ (2009) First Peoples in a New World. Colonizing Ice Age America. Univ of California Press.
31. HinchAG, TandonA, PattersonN, SongY, RohlandN, et al. (2011) The landscape of recombination in African Americans. Nature 476 : 170–175.
32. KongA, GudbjartssonDF, SainzJ, JonsdottirGM (2002) A high-resolution recombination map of the human genome. Nature 31 : 241–247.
33. AutonA, Fledel-AlonA, PfeiferS, VennO, SégurelL, et al. (2012) A fine-scale chimpanzee genetic map from population sequencing. Science 336 : 193–198.
34. BlumMGB, FrançoisO (2005) Minimal clade size and external branch length under the neutral coalescent. Advances in Applied Probability 37 : 647–662.
35. MarjoramP, WallJD (2006) Fast “coalescent” simulation. BMC genetics 7 : 16.
Štítky
Genetika Reprodukční medicínaČlánek vyšel v časopise
PLOS Genetics
2014 Číslo 8
Nejčtenější v tomto čísle
- Meta-Analysis of Genome-Wide Association Studies in African Americans Provides Insights into the Genetic Architecture of Type 2 Diabetes
- KDM6 Demethylase Independent Loss of Histone H3 Lysine 27 Trimethylation during Early Embryonic Development
- The RNA Helicases AtMTR4 and HEN2 Target Specific Subsets of Nuclear Transcripts for Degradation by the Nuclear Exosome in
- EF-P Dependent Pauses Integrate Proximal and Distal Signals during Translation
Zvyšte si kvalifikaci online z pohodlí domova
Současné možnosti léčby obezity
nový kurzVšechny kurzy








