Determinative Developmental Cell Lineages Are Robust to Cell Deaths
It is widely believed that development plays an important role in the phenotypic robustness of organisms to environmental and genetic perturbations. But, the developmental process and cell fate are largely predetermined and fixed in some species, including for example mollusks, annelids, tunicates, and nematodes. How these organisms deal with perturbations that cause cell deaths in ontogenesis has been a long-standing puzzle. We propose and demonstrate that the developmental cell lineages of these species are structured such that the resulting cellular compositions of the organisms are only moderately affected by cell deaths. A series of highly nonrandom features of the cell lineages underlie their developmental robustness and these features likely originated as adaptations in the face of various disturbances during development. Our findings reveal important organizing principles of determinative developmental cell lineages and a conceptually new mechanism of phenotypic robustness, which have broad implications for development and evolution.
Published in the journal:
. PLoS Genet 10(7): e32767. doi:10.1371/journal.pgen.1004501
Category:
Research Article
doi:
https://doi.org/10.1371/journal.pgen.1004501
Summary
It is widely believed that development plays an important role in the phenotypic robustness of organisms to environmental and genetic perturbations. But, the developmental process and cell fate are largely predetermined and fixed in some species, including for example mollusks, annelids, tunicates, and nematodes. How these organisms deal with perturbations that cause cell deaths in ontogenesis has been a long-standing puzzle. We propose and demonstrate that the developmental cell lineages of these species are structured such that the resulting cellular compositions of the organisms are only moderately affected by cell deaths. A series of highly nonrandom features of the cell lineages underlie their developmental robustness and these features likely originated as adaptations in the face of various disturbances during development. Our findings reveal important organizing principles of determinative developmental cell lineages and a conceptually new mechanism of phenotypic robustness, which have broad implications for development and evolution.
Introduction
Phenotypic robustness, often referred to as canalization, is the phenomenon that a phenotypic trait is invariant in the face of environmental or genetic perturbations [1]–[7]. Phenotypic robustness allows the maintenance of high fitness even under suboptimal conditions, which are not uncommon in nature [1]–[7]. Phenotypic robustness may also facilitate adaptation under certain conditions [8]. The genetic basis of phenotypic robustness has been of long-standing interest, and several underlying mechanisms have been elucidated [2], [3], [5]. For instance, capacitors such as molecular chaperones can buffer the disturbances from stressful environments and deleterious mutations; phenotypic variance is exposed upon the removal of capacitors [9], [10]. Functional redundancy in genetic systems is another cause of robustness because it renders the phenotype of an organism relatively invariant to the loss of a genetic component. Such redundancies are known to exist at both the individual gene level (e.g., between duplicate genes) [11] and the systems level (e.g., between alternative metabolic pathways) [5], [12]. Several evolutionary mechanisms explain the origin and maintenance of such functional redundancies and the resulting robustness [12]–[15]. Other proposed mechanisms of robustness include expression regulation via transcriptional regulatory networks [16], posttranscriptional regulation by microRNA [17], [18], and certain feedback/feed-forward circuits in signaling among cells [19].
It has long been recognized that ontogenesis, or the development of an organism from a fertilized egg to an adult, is a key component of phenotypic robustness [1]. But the mechanism underlying the ontogenic robustness is not well understood. Regulative development, where rescuing processes may be triggered in response to cell deaths caused by environmental or genetic perturbations, could ensure ontogenic robustness. However, regulative development usually accompanies massive cell rearrangements and migration before or during cell fate specification [20], which is not a desirable feature in species or tissues that have short developmental time, let alone the complex genetic or cell-cell communication network required for the regulation. In fact, no embryo displays only regulative development [20]. Even in largely regulative embryos, one finds determinative (also known as mosaic) development [20], where the developmental process and cell fate are fixed. In invertebrate embryos, especially those of mollusks [21], annelids [22], tunicates [23], and nematodes [24], [25], determinative development is extensively observed [20]. How do these species deal with environmental or genetic perturbations in ontogenesis? To answer this question, we investigate the ontogenic robustness of three invertebrates dominated by determinative development, using developmental cell lineages that describe the exact genealogical relations of all cells of an individual embryo or adult. We show that the determinative development of these invertebrates is highly robust to two types of cell death, which approximate the effects of random environmental disturbances (or somatic mutations) and genetic disturbances (i.e., germline mutations), respectively. We identify multiple extremely nonrandom features of the cell lineages that explain the ontogenic robustness, and show by evolutionary simulation that this characteristic can arise as an adaptation to certain disturbances in ontogenesis.
Results
Quantifying the robustness of determinative developmental cell lineages
A typical developmental cell lineage takes the form of a binary tree composed of nodes and branches (Fig. 1A). The nodes represent cells, whereas the branches show descendant relationships among cells. There are two categories of nodes: terminal and internal. Terminal nodes represent cells at the final stage of the developmental process represented by the cell lineage, which may or may not be the final stage of development. Terminal cells are the ultimate product of the ontogenesis represented by the cell lineage. By contrast, internal nodes represent direct or indirect progenitors of the terminal cells, which are produced through differentiation and proliferation of the internal nodes. Here we consider only those cell lineages that start from the zygote.
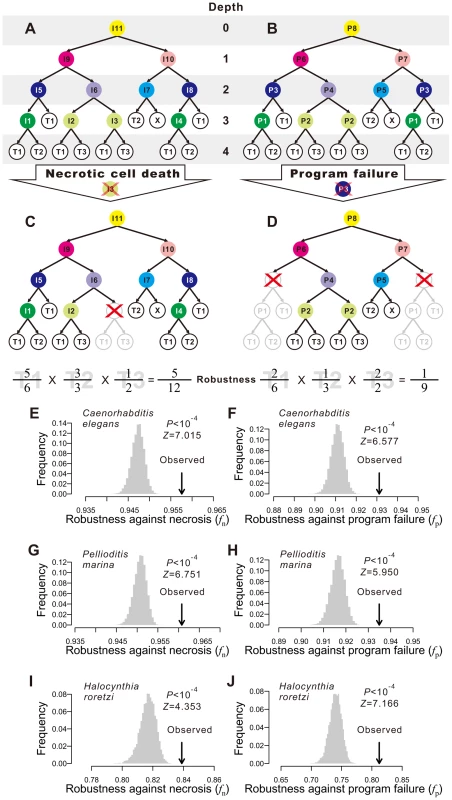
In organisms such as the nematode worm Caenorhabditis elegans, cell fate determination is generally autonomous such that dead or degenerated cells are rarely replaced or compensated by other cells [25]. In other words, the cell lineage and the identity of each cell in the lineage are essentially invariable among individuals. We first classify the terminal cells in a cell lineage into different functional types [25], [26]; cells of different types perform distinct physiological functions whereas cells of the same type perform similar functions. From a cellular perspective, the ultimate consequences of both environmental and genetic disturbances to ontogenesis may be largely represented by the loss of certain terminal cells, although other consequences also exist (see Discussion). Because of the distinct functions of different terminal cell types, it is reasonable to assume, to a first approximation, that the probability of an organism to survive and reproduce is determined by the product of the weighted fraction of live terminal cells of each cell type. That is,
where T is the total number of terminal cell types except apoptotic cells, Ni is the number of terminal cells of type i in the absence of any disturbance, ni (ni≤Ni) is the actual number of live terminal cells of type i, and ai≥1 is an exponent reflecting the relative importance of cell type i to organismal growth and reproduction. For simplicity, we describe our results using ai = 1 for all i. Using other ai values yields similar results (Figs. S1A–F). Here f can be viewed as a measure of developmental robustness to cell deaths. While f is likely a component of Darwinian fitness, it is not equivalent to fitness.Impacts of environmental and genetic perturbations on cell lineages manifest as the loss of internal and terminal cells. When an internal cell dies, all of its direct and indirect descendant cells are regarded as lost. We consider two types of perturbation. The first type is referred to as necrosis [27] or simply random cell death. This type of lineal perturbation mimics environmental disturbances or somatic mutations that lead to accidental deaths of individual cells. Note that our use of necrosis is different from that in some literature where it also includes cell death caused by germline mutations [27]. The second type of perturbation is referred to as division program failure (see Fig. 1B and below for the definition of cell division programs), which mimics germline mutations that cause the deaths of all cells that use a particular genetic program for cell division. We consider all internal cells that use the failed program to be arrested, resulting in the loss of all direct and indirect descendants of these internal cells. The two types of perturbation only approximate environmental disturbances (and somatic mutations) and genetic disturbances (i.e., germline mutations), respectively, because of several kinds of exceptions (see Discussion). Let fn and fp be the f value in the presence of necrosis and program failure, respectively. To estimate fn, we first calculate f when one non-root cell and all of its descendants are removed (Fig. 1C). We repeat this process for every non-root cell in the lineage and calculate the mean resulting f, which is the expected lineage robustness to the death of a randomly chosen non-root cell. A real cell lineage is said to be robust to necrosis if its fn is significantly higher than that expected from a randomized cell lineage that produces the same terminal cells.
To estimate fp, we follow a previous definition of cell division programs [26]. Every cell division in the lineage produces two daughter cells from a parental cell. The program used in the division is defined entirely by the types of the daughter cells. Here, a daughter cell may be terminal or internal, meaning that its type may be a terminal cell type or a division program (see node colors in Figs. 1A, B). Thus, two internal cells that give rise to the same types of daughter cells use the same program. For example, node I5 and I8 in Fig. 1A both use the program P3 (Fig. 1B). This definition is supported by the observation that the transcriptome of a cell is largely determined by the cell fate rather than the lineal history [28]. We traverse the entire cell lineage to define all division programs. If one program fails, all internal cells that use the program and all of their descendant cells are lost (Fig. 1D). We thus estimate fp by calculating the expected f using Eq. (1), with a specific per-program rate of failure being 1 over the number of internal cells (see Materials and Methods). A cell lineage is said to be robust to program failure if its fp is significantly greater than that expected from a randomized cell lineage that produces the same terminal cells.
Determinative developmental cell lineages are robust to both necrosis and program failure
We used determinative developmental cell lineages starting from the zygote and up to a >100-cell stage. To our knowledge, such lineages have been completely described in only three animal species: Caenorhabditis elegans, Pellioditis marina, and Halocynthia roretzi. Previously reported developmental cell lineages of other species are incomplete in internal or terminal cells on the lineage tree, their mother/daughter relationship, and/or functional categorization of terminal cells, and thus cannot be analyzed here (Table S2). Among the three species to be analyzed here, the nematode C. elegans is the first animal with its developmental cell lineage mapped at the single cell resolution [25]. Here we use the C. elegans cell lineage producing 671 terminal cells during the hermaphrodite embryogenesis, and categorize the terminal cells by standard anatomical descriptions [26], [29]. P. marina is another nematode, but lives in the sea. The cell lineage of P. marina, followed up to muscle contraction, has 638 terminal cells [24], [26]. H. roretzi, commonly known as the sea squirt, is an ascidian. We use the cell lineage of H. roretzi up to the 110-cell stage in this study [26], [30]. Hence, our analysis includes representatives from both Protostomia (C. elegans and P. marina) and Deuterostomia (H. roretzi), the two subgroups of triploblastic animals.
We estimated fn and fp of each of the three cell lineages by considering necrosis (Figs. 1E, G, I) and program failure (Figs. 1F, H, J), respectively. To compare with each real lineage, we generated 10,000 random cell lineages under the assumption that, at any developmental stage, all terminal cells have the same probability of cell division. Computationally, each of these random lineages was created by randomly coalescing the terminal cells of the real lineage exactly two cells at a time (Fig. S2). We found that fn and fp are significantly greater in each of the three real lineages than in their corresponding random lineages (P<0.0001; Figs. 1E–J), demonstrating that the three animal cell lineages are robust to both necrosis and program failure. The reduction in f (from 1) caused by necrosis is on average 19.6, 20.4, and 12.1% smaller in the three real lineages, compared with their respective random lineages. The corresponding numbers are 22.8, 22.2, and 27.8% for program failure. If the terminal cells of the same functional type are not equally important [31], one could divide a cell type into subtypes when estimating fn and fp, which would also result in more cell division programs. To evaluate the impact of considering subtypes of terminal cells and division programs on our results, we divided C. elegans neurons into five subtypes [26] and altered the definition of division programs correspondingly. The results, however, are qualitatively unaltered (Figs. S1G, H). We also examined an expanded hermaphroditic C. elegans cell lineage that includes post-embryonic cells, totaling 937 terminal cells, and the results are similar (Figs. S1I, J). One assumption made in our analysis is that all cells (or programs) have the same probability of necrosis (or failure). To investigate the impact of this assumption, we allowed different cells (or programs) to have different rates of necrosis (or failure) that follow an exponential distribution with the mean of the distribution identical to the constant rate used above. The obtained results are, however, similar (Fig. S1K, L), suggesting that our results are not sensitive to the assumption of equal necrosis (or program failure) rates. Because the overall results from the three species are similar, from now on, we present our findings from C. elegans in the main figures and those from the other two species in the accompanying supplementary figures.
Shallowness of the cell lineages contributes to their robustness
To understand the underlying mechanisms of the observed lineage robustness to necrosis and program failure, we examined various characteristics of both the real and random cell lineages. Let us define the depth of a cell in a cell lineage by the number of cell divisions required to generate the cell from the root, which is the zygote in the lineages analyzed here. To a terminal cell, the smaller its depth, the lower the probability of its loss, because each cell division carries risks of necrosis and program failure. Hence, reducing the depths of terminal cells should improve f.
Let us define the maximum depth of a cell lineage by the largest depth among all terminal cells in the lineage. Indeed, the maximum depth is significantly smaller in the three real lineages, compared with their corresponding random lineages (Fig. 2A; Figs. S3A, B). The theoretical minimum of the maximum depth of a cell lineage with a total of L terminal cells is [log2L], where the square bracket represents the minimal integer that is no smaller than the number inside. The theoretical minimum of the maximum depth is 10, 10, and 7 for the three real lineages, respectively. The observed maximum depth is 12, 11, and 7, respectively, indicating that the real maximum depth is either identical to or close to the theoretical minimum. By calculating fn and fp of random lineages with different maximum depths, we found that, on average, fn and fp both increase as the maximum depth decreases (Figs. 2B, C; Figs. S3C–F), suggesting that reducing the maximum depth of a cell lineage tends to increase its robustness to necrosis and program failure. Intriguingly, the real lineages have significantly greater fn and fp than the random lineages with the same maximum depths (Figs. 2B, C; Figs. S3C–F), revealing the presence of additional factors that contribute to the high fn and fp of the real lineages.
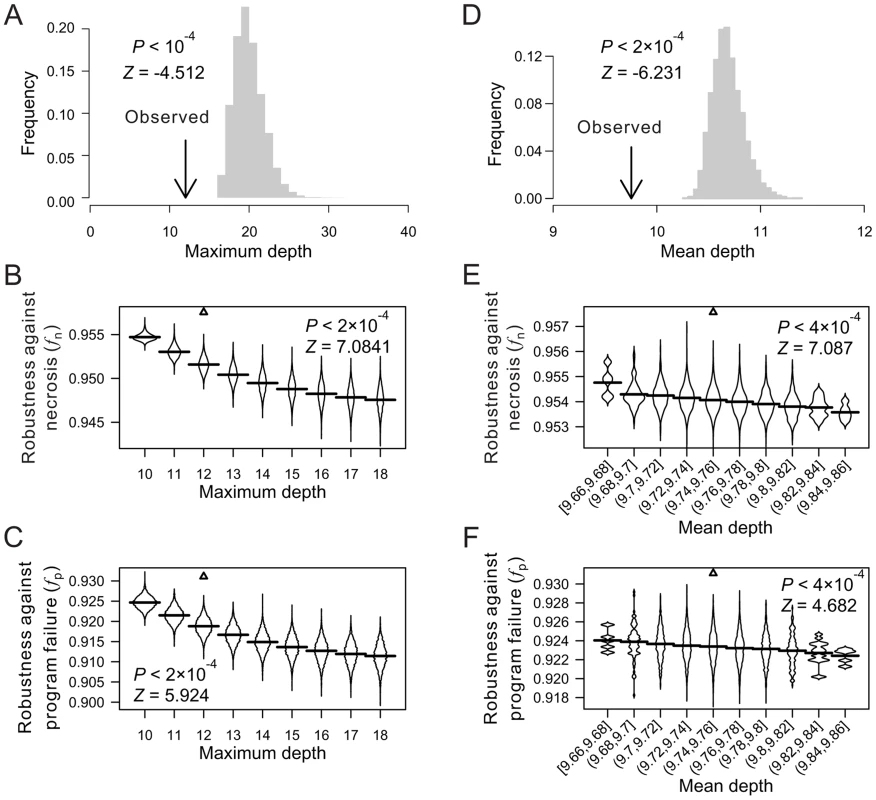
We found the mean depth of all terminal cells in each of the three real lineages to be significantly smaller than that of their corresponding random lineages even when the maximum depths of these random lineages are fixed at the observed values (Fig. 2D; Figs. S3G, H). For each real lineage, we then generated 10,000 random lineages that have the maximum depth identical to the observed value and the mean depth similar to the observed value (See Materials and Methods). The mean depth is found to impact fn and fp negatively even when the maximum depth is fixed (Figs. 2E, F; Figs. S3I–L), confirming that a smaller-than-expected mean depth given the maximum depth is another contributor to the high fn and fp of the real lineages. Nonetheless, the real lineages still have greater fn and fp than the random lineages of the same maximum and mean depths (Figs. 2E, F; Figs. S3I–L), suggesting that additional factors contribute to the high fn and fp of the real lineages.
Lineal topology and organization of terminal cells contribute to robustness
When the depths of all terminal cells are fixed, the only thing in a cell lineage that can vary is the lineal topology. Here, the term “topology” is equivalent to that in phylogenetics, including both the lineage tree structure when the terminal cells are unlabeled and the arrangement of the labeled terminal cells given the tree structure. To test the impact of lineal topology on robustness, for each real lineage, we generated 10,000 random lineages with varying topologies but the same depth distribution as in the real lineage for all terminal cells. Again, fn and fp are significantly greater in the real lineages than in their respective randomized lineages (Figs. 3A, B; Figs. S4A–D), demonstrating the contribution of lineal topology to the high robustness of real lineages.
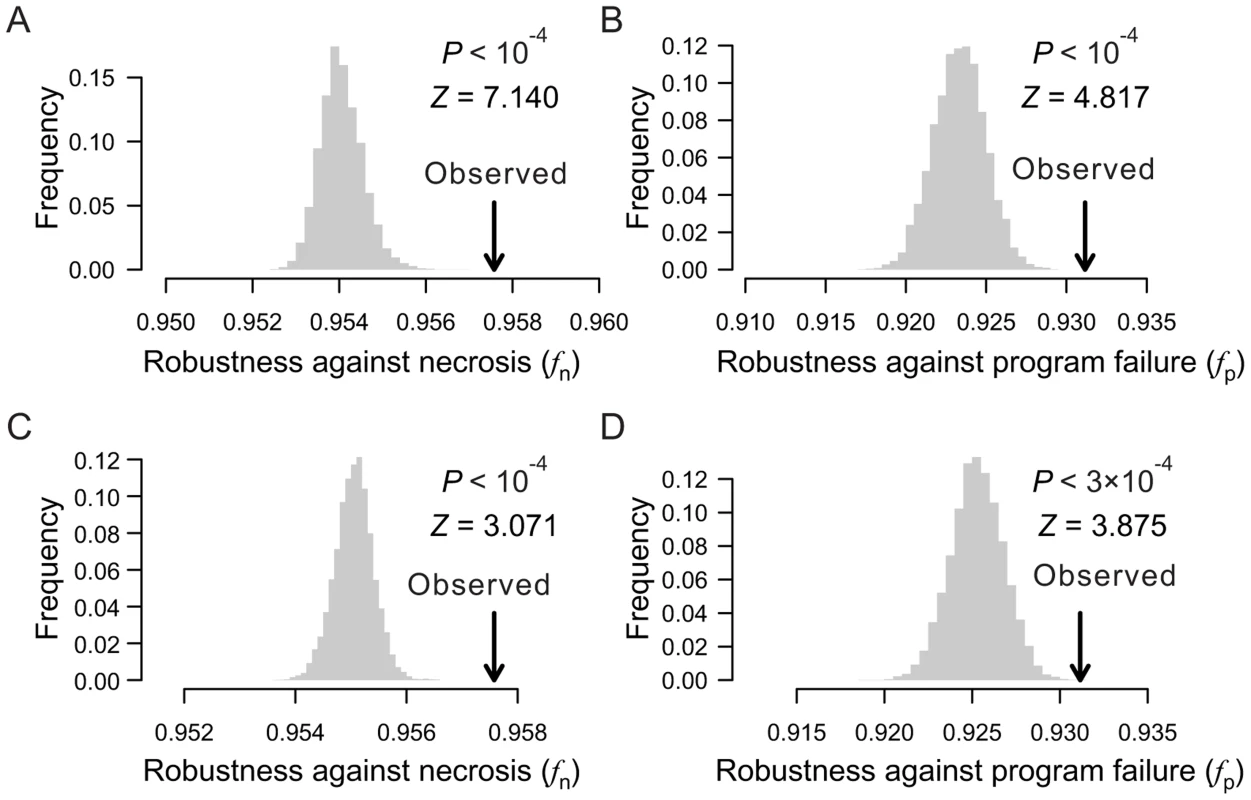
Furthermore, fn and fp are significantly greater in each real lineage than in its corresponding random lineages that share the same tree structure, which were generated by relabelling the terminal cells in the real lineage (Figs. 3C, D; Figs. S4E–H). Thus, the organization of terminal cells contributes to the robustness of the real lineages.
Early appearances of rare cells improve robustness
What features of the terminal cell organization underlie the high robustness of the real lineages? As mentioned, terminal cells have been classified into functional types. We define the size of a cell type by the number of terminal cells belonging to the type. Cells of large cell types are referred to as common cells, whereas those of small cell types are referred to as rare cells. According to Eq. (1), loss of a rare cell has a larger adverse impact on f than the loss of a common cell. Because a low-depth terminal cell is less likely than a high-depth terminal cell to be lost, one strategy to improve f, given the lineage tree structure, is to arrange the terminal cells in such a way that the rare cells have relatively low depths and common cells have relatively high depths. Indeed, in each of the three real lineages, a positive correlation exists between the depth of a terminal cell and the size of its cell type (see binned results in Fig. 4A; Figs. S5A, B). This correlation (ρrare-early) is significantly stronger than the chance expectation, which is calculated using 10,000 lineages constructed by randomly relabelling the terminal cells of each real lineage (Fig. 4B; Figs. S5C, D). A comparison among the random lineages shows that fn and, to a much lesser degree, fp increase with ρrare-early (Figs. 4C, D; Figs. S5E–H), confirming the prediction that early appearances of rare cells in a lineage render the lineage more robust.
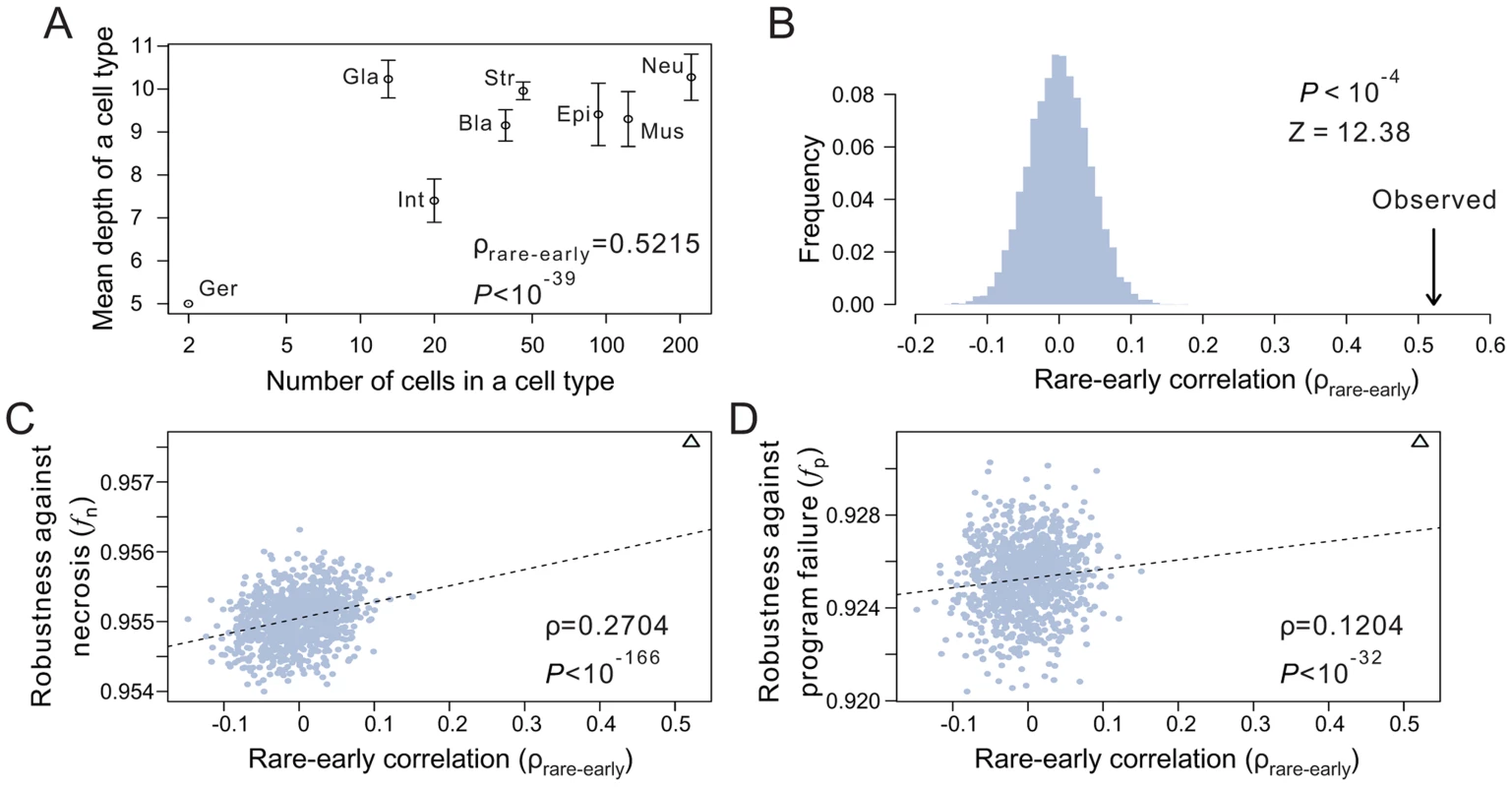
The above analysis depends critically on the classification of terminal cells. For instance, if the late-appearing neuron cells are divided into many subtypes, the rare-early correlation would be weakened. It is thus important to classify terminal cells objectively. To this end, we analyzed the recently published single-cell expression levels of 93 genes in 363 cells of the L1 stage larvae of C. elegans [28]. Three of the 363 cells are not terminal cells in the lineage considered here and are thus removed. We then classified the remaining 360 terminal cells into eight types (Fig. S5I) based on transcriptome similarities among cells (see Materials and Methods), because the terminal cells of the C. elegans lineage analyzed here were previously classified into eight functional types after the removal of apoptotic cells [26], [29]. Although the new classification differs substantially from the previous classification (Fig. S5I), the rare-early correlation in the C. elegans lineage remains highly significant under the new classification (P<0.0001, compared with 10,000 random lineages with the same lineage tree structure; Fig. S5J), and this result is insensitive to the number of cell types classified (from 4 to 40) (Fig. S5K). Because only 360 of the 671 terminal cells in the C. elegans lineage analyzed here have the single-cell gene expression data, the new cell type classification is incomplete and hence cannot be used to calculate fn and fp (see Table S1). But, because cell type reclassification does not alter the shallowness and tree structure of the lineage and because the rare-early correlation clearly remains unchanged, the reclassification should not qualitatively affect fn and fp.
Besides its contribution to robustness, the rare-early correlation has other potential implications. For instance, the risk of mutation is minimized for cells that appear early. In the case of the C. elegans cell lineage analyzed here, the early appearance of the two germ cells may have reduced the germline mutation rate per nematode generation. Note, however, that the rare-early correlation is unlikely to have been caused by natural selection for a low germline mutation rate, because the correlation remains strong (ρ = 0.515; P<10−38) even when the germ cells are not considered. A potential alternative explanation of the rare-early correlation is that the rare cells have physiological roles to support the developing embryo and hence need to be produced earlier. However, this hypothesis does not appear to be empirically supported. For example, the two germ cells that appear very early in the cell lineage have no physiological role in supporting the developing embryo.
Non-clonality of cell types contributes to robustness
Intuitively, one may think that cell types are clonal, meaning that all terminal cells of a cell type form a monophyletic or paraphyletic group in a cell lineage tree [32], [33]. This intuition, however, is incorrect. Studies in multiple animal species have shown that cell types are typically nonclonal or polyphyletic [34]–[41], meaning that the terminal cells of the same cell type are derived from multiple sublineages (e.g., see Fig. 1A). If we compare two cell lineages with the same tree structure, an internal cell death will kill the same number of terminal cells in the two lineages, but the dead terminal cells are more likely to be of the same type in the clonal lineage than in the non-clonal lineage. Because the loss of multiple terminal cells of the same type tends to result in a lower f than the loss of the same number of terminal cells distributed among several types (see Materials and Methods), we predict that clonality reduces lineage robustness while non-clonality improves lineage robustness.
To test the above hypothesis, let us measure the clonality of a cell lineage by
where T is the total number of terminal cell types, M represents all pairs of terminal cells, where a subscription of i limits the cell pairs within cell type i, and dj is the lineal distance between cell pair j, which is the number of edges on the shortest path connecting the cell pair (e.g., the lineal distance between the two T3 cells in Fig. 1A is 4). For a given lineage tree structure, in the equation is fixed, whereas decreases with clonality. Thus, the stronger the clonality, the larger the C.To examine the role of clonality on robustness, we controlled all known lineage features that contribute to robustness. Specifically, from a real cell lineage, we rearranged the terminal cells without altering their respective depths and generated a series of random lineages with different levels of clonality (see Materials and Methods). We found that (i) C is lower in the three real lineages (triangles in Fig. 5A; Figs. S6A, B) than in the corresponding random lineages where all cell types are as clonal as possible given the constraints of the lineage tree structure and cell depths (purple dots; P<0.12, 0.02, and 0.02, respectively) and (ii) a decrease in C leads to an increase in lineage robustness to both necrosis (Fig. 5A; Figs. S6A, B) and program failure (Fig. 5B; Figs. S6C, D). These observations support our hypothesis that the non-clonality of the real lineages improves their robustness. Notably, the non-clonality, in combination with the previously identified lineage features, seems sufficient to explain the observed robustness of the real lineages (Fig. 5A, B).
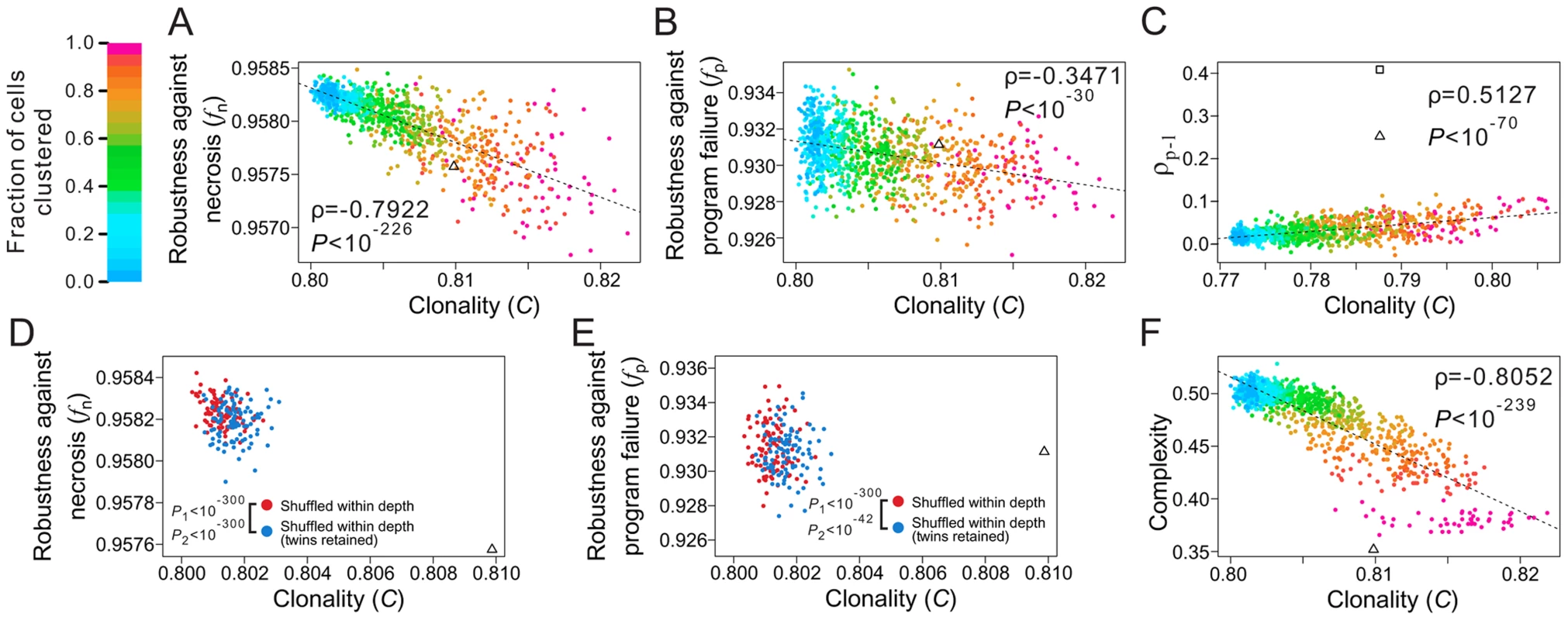
A potential alternative explanation of the non-clonality of the real lineages is that it is dictated by some spatial requirements for terminal cells. Because not all cells of the same type are physically proximate (e.g., epithelial cells on the two hands of a person) and because cells may possess limited abilities to migrate, be costly to migrate, and/or have reduced migration under natural selection for rapid development [24], [42], some cell types are necessarily non-clonal. To examine whether some spatial requirements have dictated the reduction of the clonality of the real lineages and as a result created the observed robustness as a byproduct, we obtained the three-dimensional spatial coordinates of terminal cells in C. elegans [43]. We then calculated Spearman's rank correlation (ρp-l) between the physical distance and lineal distance for all pairs of terminal cells that belong to the same type (see Materials and Methods). The C. elegans lineage indeed has a much greater ρp-l (triangle in Fig. 5C) when compared with the above generated random lineages of similar C (dots in Fig. 5C). Nevertheless, the C. elegans ρp-l is apparently not maximized, because we were able to acquire an even higher ρp-l by rearranging the terminal cells of the C. elegans lineage within their respective depths (square in Fig. 5C). More importantly, a comparison among the above generated random lineages shows that ρp-l tends to increase with C, suggesting that lowering C does not help raise ρp-l. In other words, the observed low clonality cannot be explained by the spatial requirements.
Notwithstanding, the C value of each real lineage remains significantly greater than that when all of its terminal cells are completely randomly situated within their respective depths (dark blue dots in Fig. 5A; Figs. S6A–B; P<0.02 in all three species). Two factors may have constrained the further reduction of C and the further rise of robustness in the real lineages. The first potential constraint arises from a demand for spatial proximity of certain terminal cells of the same type. Because cell migration is limited [24], [42] and because some cell types exert their functions through physical connections such as in the neural system and muscles, there is a requirement for a large number of terminal cells of the same type to be produced next to one another, which hinders a further reduction of C. To test this hypothesis, we focused on pairs of terminal cells that share their immediate progenitor as well as their cell type. By analyzing the spatial coordinates of terminal cells, we found that such “twin” terminal cells are significantly closer physically to each other than each is to other cells of the same type (Z = −15.32, P<10−52; see Materials and Methods), suggesting that the existence of such “twin” terminal cells is in part a result of the spatial requirements. There are also significantly (P<10−4) more twin terminal cells in C. elegans (155) than the random expectation (59.4), which is estimated by randomly rearranging terminal cells within their respective depths. To examine if this spatial requirement constrains the reduction of clonality and the rise of robustness, we retained the relationship of twins while randomly rearranging the terminal cells within their respective depths. In support of our hypothesis, a greater C and smaller fn and fp are observed after this type of rearrangement (blue dots in Figs. 5D, E and Figs. S6E–H), compared with the rearrangement without the twin constraint (red dots).
The second potential constraint is lineage complexity [26], which is the number of division programs used in the lineage, as shown in Fig. 1B. Azevedo and colleagues suggested that lineage complexity has been selectively minimized in evolution [26]. Because lineage complexity negatively correlates with C (Fig. 5F; Figs. S6I, J), selection for lower complexity is expected to increase clonality and hence decrease lineage robustness.
Taken together, our analyses revealed lower-than-expected clonalities in the real cell lineages, which have likely resulted from the potential selection for lineage robustness. Why the clonalities are not further reduced may be explained by the spatial constraints of certain cells and the possible selection for lineage simplicity.
Natural selection can generate the observed robustness of developmental cell lineages
We have demonstrated the robustness of the three animal cell lineages to necrosis and program failure and have identified a number of lineage features or mechanisms that underlie the observed robustness. But how did such lineage robustness originate? It is not obvious that natural selection for high robustness during the evolutionary expansion of cell lineages will result in high robustness, because today's lineage is greatly restricted by its ancestral forms. For instance, 577 terminal cells have the same fate in the lineages of the two nematodes C. elegans (671 terminal cells) and P. marina (638 terminal cells) [26]. Below we investigate by computer simulation if the observed robustness of the three cell lineages is achievable simply by adaptation to necrosis or program failure during the evolutionary expansion of cell lineages.
Our simulation, named “macroevolution”, mimics the expansion of a cell lineage in macroevolution by stepwise additions of new terminal cells via divisions of existing terminal cells. That is, upon a division, one daughter cell inherits the identity of its parental cell while the other evolves into a new cell type (see Materials and Methods). Our simulated lineages are the same as the real lineages in the number and identities of terminal cells, but differ in lineal topology and terminal cell depths. Different intensities of selection for high fn or high fp are applied during the course of the macroevolution. The actual evolution of developmental cell lineages does not necessarily proceed as our macroevolution simulation, because cell fate may change in evolution [24]. In other words, the actual evolution of developmental cell lineages may be more flexible and our overly-constrained macroevolution likely reveals the lower limit of robustness achievable under natural selection for robustness.
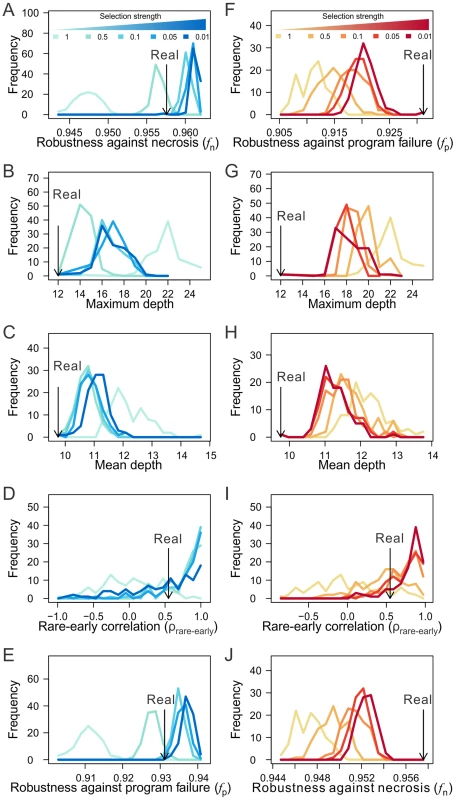
We found that selection for high fn can result in lineages that have similar levels of fn as observed in the real lineages (when the selection intensity is 0.5), while removing the selection results in lineages of much lower fn (Fig. 6A; Figs. S7A, K). Compared with the lineages generated under no selection, those generated by selecting for high fn exhibit the features known to improve fn, including the lineage shallowness (although slightly less extreme than in the real lineages) and rare-early correlation (Figs. 6B–D; Figs. S7B–D, L–N). Clonality C is not compared because it is not comparable among lineages with different tree structures. Intriguingly, selection for high fn also increases fp (Fig. 6E; Figs. S7E, O). On the contrary, selection for high fp fails to recapitulate the observed level of fp or fn (Figs. 6F, J; Figs. S7F, J), except in the case of the H. roretzi lineage (Figs. S7P, T), which may be too small to be informative. While selection for high fp does result in shifts of the robustness-enhancing lineage features in the predicted directions, these shifts tend not to reach the levels observed in the real lineages (Figs. 6G–I; Figs. S7G–I, Q–S; see Discussion). These findings reveal the possibility that the higher-than-expected fn and fp in the real lineages are both due to natural selection for high fn. In other words, the observed high fp in the real lineages is probably a byproduct of the selection for high fn. Consistent with this conclusion is the finding that fn and fp are highly positively correlated among various randomized lineages generated from the real lineages (Figs. S7U–W). While our simulation does not prove that the higher-than-expected fn and fp in the three animal cell lineages are caused by selection for fn, it does provide strong evidence for the viability of the hypothesis.
Lineage robustness is unexplainable by natural selection for lineage simplicity
When rearranging terminal cells of a real lineage within their respective depths, we showed that increasing lineage clonality reduces lineage robustness (Figs. 5A, B) and complexity (Fig. 5E), implying a positive correlation between robustness and complexity. A more extensive analysis, however, revealed that the correlation between robustness and complexity may be positive or negative, depending on the groups of random lineages compared (Figs. 7A, B). For example, comparing lineages generated by shuffling terminal cells within their respective depths (red dots in Figs. 7A, B and Figs. S8A–D) and those generated by completely shuffling all terminal cells (green dots), we found that the rare-early correlation increases robustness but decreases complexity. By contrast, when we compare the lineages generated by within-depth shuffling with (blue dots in Figs. 7A, B and Figs. S8A–D) or without (red dots) retaining twin terminal cells, we found a positive correlation between robustness and complexity, suggesting that the spatial constraint of terminal cells decreases complexity at the cost of robustness.
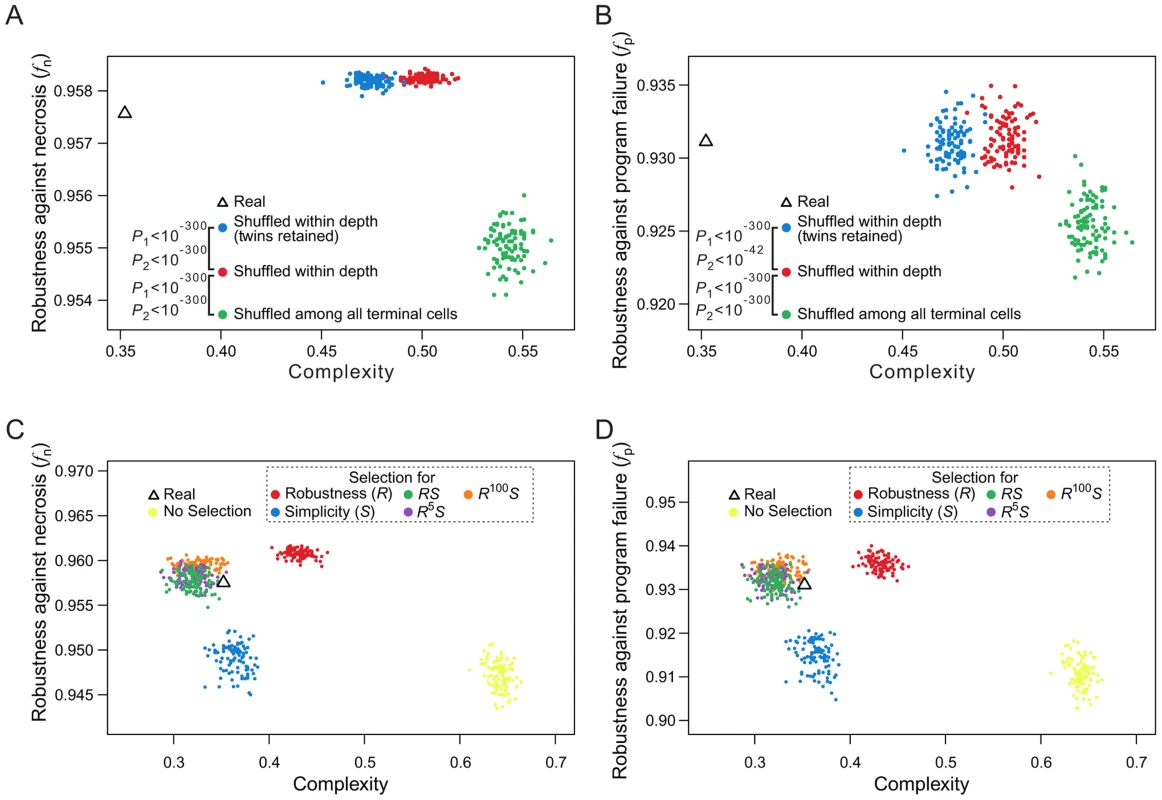
Because lineage robustness and complexity are sometimes negatively correlated, selection against complexity (or for simplicity) [26] may result in high robustness, and vice versa. We thus used our macroevolution simulation with relatively strong selection (intensity = 0.05) to investigate if selection for robustness to necrosis or simplicity alone can account for both the robustness and simplicity of the real lineages. To investigate the interplay between robustness and simplicity, we used different fitness functions in the macroevolution simulation with different weights for robustness (R) and simplicity (S) (dash-lined box in Figs. 7C, D; Figs. S8E–H, where the relative weights for R and S are reflected by the power of R; see Materials and Methods for details). Four observations were made (Figs. 7C, D; Figs. S8E–H). First, selection for simplicity alone enhances simplicity but not robustness (fn or fp), suggesting that robustness cannot be a byproduct of selection for simplicity (blue dots in the figures). Second, selection for robustness to necrosis alone enhances robustness (fn and fp) as well as simplicity (red dots). Nevertheless, the resulting lineages are still more complex than the real lineages, suggesting that the simplicity of the real lineages may be partially but not entirely due to selection for robustness to necrosis. Third, simultaneous selections for both robustness and simplicity can generate lineages that are similar to the real lineages in fn, fp, and simplicity (green, purple, and orange dots), supporting the actions of both selective forces in the evolution of the real lineages. Fourth, under the parameters used, selection for robustness alone generates lineages that exceed the real lineages in fn and fp, whereas this disparity disappears under simultaneous selections for robustness and simplicity, supporting the notion that a requirement for simplicity prevents a further increase in robustness.
Discussion
Determinative developmental cell lineages are robust to cell deaths
Phenotypic robustness is an important characteristic of life, but its underlying mechanisms and evolutionary origins are not well understood. In this article, we demonstrated that determinative developmental cell lineages are robust to necrosis and cell division program failure, which approximately represent environmental (or somatic) and genetic (i.e., germline) disturbances, respectively. Although some germline mutations with incomplete penetrance may act like environmental perturbations and some environmental perturbations impact specific programs and hence behave like germline mutations, our analyses included both types of disturbances. We further showed by computer simulation that such robustness can arise from natural selection for robustness against necrosis during the evolutionary expansion of cell lineages. Our findings thus reveal a new mechanism of phenotypic robustness as well as its potential evolutionary origin. Different from almost all previously studied mechanisms of phenotypic robustness, which act at the subcellular or cellular levels, cell lineage robustness manifests at the supracellular level and hence is a unique feature of multicellular organisms. Our study also provides a novel explanation of the contribution of ontogenesis to phenotypic robustness.
Necrosis caused by environmental stresses or somatic mutations are unavoidable [27]. Similarly, cell division program failure is expected to occur occasionally due to germline mutations [27]. Although mechanisms buffering stresses and mutations may exist such that the rate of necrosis or division program failure is lowered [2]–[5], [44], cell lineage robustness is likely an important mechanism buffering the adverse effect of necrosis and program failure upon their occurrence. This mechanism is especially important for species whose development is predominantly determinative because the cell fate is largely fixed in these organisms. Cell lineage robustness, along with regulative development (see below), complements subcellular and cellular mechanisms of robustness to form a multi-layer defense system against environmental and genetic perturbations that are common in nature.
A highly related subject is the robustness of sublineages, which are lineages starting from non-zygote cells. Although our definition of robustness is directly applicable to sublineages, the expectation for sublineage robustness may vary, depending on the specific types of sublineages. For instance, regulative development occurs to a small number of cells during the late development of C. elegans, where cell losses may sometimes be compensated by additional divisions of neighboring cells [25]. The sublineages with the ability of such compensatory growth, conferred by regulative development, may not have the typical properties of robust lineages such as low cell depths. Compensatory growth may be further generalized to include sublineages that are populated by stem cells, commonly seen in arthropods and vertebrates [45]. Other than delaying the development, such compensatory growth can apparently solve the problems caused by necrosis [46]. The existence of compensatory growth demonstrates canalization mechanisms other than the cell lineage robustness revealed here, further supporting the importance of having a robustness developmental process. With a modification of our model, stem cells may be included such that the robustness of developmental cell lineages can be evaluated for organisms with prevalent compensatory growth.
Our findings of cell lineage robustness and its mechanisms offer important biological insights. For example, somatic-mutation-based analysis in mice revealed that cells of the same type from the same organ such as the kidney have several different lineal histories [38], [39]. We showed that this phenomenon of non-clonality is beneficial to lineage robustness, at the cost of lineage simplicity. Thus, the benefit of having increased robustness may exceed the cost of having extra division programs for these cell types. In general, features contributing to lineage robustness (e.g., rare cells are produced relatively early in ontogeny) may be found to be detrimental to other traits (e.g., common cells would have relatively high probabilities of death). Knowing the underlying tradeoffs helps understand the origins of such detrimental features, which may lead to potential solutions.
Evolutionary origins of cell lineage robustness
One intriguing finding from our macroevolution simulation is that both fn and fp can be raised by natural selection for high fn but not as effectively by selection for high fp. This disparity is not because the parameters we used render the cell death rate higher in the presence of necrosis than in the presence of program failure. In fact, the opposite is true (e.g., see Fig. 1E–J). The disparity may be related to the larger variation in fp than fn among individuals whose expected lineages under no cell death are identical. Even when the rates of necrosis and program failure are fixed, individuals with the same expected lineages can still have different f values because necrosis and program failure are stochastic. Based on the necrosis and program failure rates used here, we estimated in C. elegans that the standard deviation of fn among individuals is 0.1095, while that of fp is 0.1745. It is reasonable to assume that a larger variation in f translates into a larger variation in fitness. Because the larger the variation in fitness among (isogenic) individuals, the lower the efficacy of natural selection [47], selection for fp is less effective than selection for fn in raising lineage robustness. Nevertheless, whether the standard deviations of fn and fp are directly comparable is unclear and other explanations may exist.
Our finding that cell lineage robustness can result from natural selection for robustness, coupled with previous findings on the possibility of selection for genetic and environmental robustness [2], [3], [7], [48], suggests the likelihood that the observed cell lineage robustness against necrosis and program failure is a direct result of natural selection for robustness. Nevertheless, we cannot exclude the possibility that the observed robustness results partially or entirely as a byproduct of other selections or generative biases [49]. For example, we showed that a low maximum depth improves the robustness of a cell lineage and that the maximum depths of the three animal cell lineages are identical or close to their theoretical minimums. Although selection for robustness against necrosis may explain this phenomenon (Fig. 6B), selection for short developmental time is another possible explanation [50]. It was previously thought that the robustness-enhancing feature of non-clonality of the cell lineages of C. elegans and P. marina results from selection for rapid development that avoids the time-consuming cell migration [24]. But the recently determined nearly complete cell lineages of two other nematodes that develop slowly (Halicephalobus gingivalis and Rhabditophanes sp.) exhibit similar non-clonality [51], [52], suggesting that selection for rapid development is not the cause of the observed non-clonality in nematodes. Furthermore, selection for fast development cannot explain other robustness-enhancing features of cell lineages (e.g., early appearances of rare cell types). Given the presence of multiple robustness-enhancing features in animal developmental cell lineages, natural selection for robustness is a plausible and the most parsimonious explanation of the origin of lineage robustness. The generative bias hypothesis would assert that the observed high robustness of developmental cell lineages is caused by mutational biases. But it is difficult to imagine that such biases would generate multiple nonrandom features that all happen to increase lineage robustness.
Limitations and future improvements
Our estimation of cell lineage robustness is based on several assumptions. First, we used a necrosis rate of one cell per lineage and a program failure rate of 1/Ninternal per program, where Ninternal is the total number of internal cells in the lineage. These parameters are probably lower than the actual rates, rendering our estimates of cell lineage robustness conservative. Our results should be verified in the future with the real necrosis and program failure rates when they become available. It is also possible that the rate of necrosis and that of program failure vary among cells and programs [53]. Such information, when it becomes available, can be incorporated into our model (Fig. S1K, L) to achieve a more accurate estimate of cell lineage robustness.
Second, the robustness function, as described by Eq. (1) under ai = 1, may not be accurate, because of (i) variable importance of cells of different types, (ii) imprecise cell type classification, (iii) interactions among different cell types, and/or (iv) potential compensation of cell death by other mechanisms. Yet, our conclusion appears robust to variable impacts of different cell types, because the use of different ai values yielded similar results (Fig. S1A–F). Our conclusion is also highly robust to cell type classification, because transcriptome-based and function-based classifications yielded similar results that are invariant to the number of cell types classified (Figs. S5I–K). Further division of a cell type into subtypes did not alter our results (Fig. S1G, H). Our results also appear to be robust to the variation in the necrosis rate among cells or the failure rate among programs (Figs. S1K–L). While necrotic cell death is rarely compensated by regeneration of the corresponding live cells in C. elegans [25], this may not be the case in some complex organisms especially during late development [46]. Similarly, it is possible that only some but not all descendants of an affected internal cell get lost. By contrast, when cell induction or replacement occurs in cell fate determination, a cell death may lead to the loss of terminal cells that are non-descendants of the dead cell. Furthermore, a perturbation may induce the production of extra terminal cells (e.g., by blocking apoptosis [54]). These variations, as well as potential interactions among different cell types, have not been considered in our analyses, but can be studied in the framework developed here when detailed information about these processes becomes available.
Third, it is possible that the potential type of an internal cell (i.e., its division program) is limited genetically, but such a constraint is not explicitly modeled in our randomization of cell lineages. With a better understanding of this constraint, we can refine our randomization in the future. Nonetheless, it is worth mentioning that the expression profiles of 93 genes examined in C. elegans terminal cells were found to be largely determine by their cell types [28], suggesting that the division programs of internal cells are not so limited, because otherwise the transcriptomes of the terminal cells should be dictated by their lineal histories.
By progressively constraining various features of a cell lineage, we identified several contributors to lineage robustness, including terminal cell depths, lineal topology, early appearances of rare cells, and non-clonality of cell types. Although the impacts of any two of these characteristics to lineage robustness are not completely overlapping, it is important to note that they are not completely non-overlapping either. As such, it is difficult to assess the relative contributions of these characteristics to lineage robustness. Although all of these characteristics exist in the three animal cell lineages examined, variations are expected when additional species are examined. For instance, in most organisms, primordial germ cells are set aside early in development [55]. In mice, however, these cells appear at a much later stage [40], [56], which likely reduces the rare-early correlation and the cell lineage robustness. But, mouse blastomeres up to the eight cell stage are equipotent [57], which reduces clonality and increases lineage robustness.
Using the macroevolution simulation, we showed that, in the evolutionary expansion of cell lineages, adaptation to random necrosis can result in highly robust cell lineages. Our simulation is a coarse-grained approximation rather than a precise description of the evolution of developmental cell lineages. However, because our simulation explicitly models historical contingency, the constraint imposed by ancestral lineages on future lineages, our simulation is more realistic than that by swapping sublineages in a real or random lineage [26]. Our model can be further improved by including the genetic networks that underlie cell fate determination [49] when such information becomes available. It can also be improved by allowing lineages to expand through divisions of internal cells rather than only terminal cells.
Outlook
Decoding the developmental cell lineages of the human and other organisms is a grand scientific challenge (http://www.lineage-flagship.eu/). With the rapid advancement of genomics [58], especially single-cell genome sequencing [59]–[61], it will not be long before one can use somatic mutations accumulated during ontogenesis to reconstruct the cell lineages of complex organisms such as mammals [62], [63]. Our computational analysis of the three determinative cell lineages provides experimentally testable [39] hypotheses on the organizing principles of developmental cell lineages and opens the door toward characterizing systemic properties of complex cell lineages, an area that promises to be of both theoretical and applied values in understanding evolution, development, and carcinogenesis.
Materials and Methods
Developmental cell lineages
To reliably evaluate lineage robustness as defined in Eq. (1) of the main text, the cell lineage data must satisfy the following four criteria (Table S1). First, the lineage has the form of a binary tree. Second, the lineage starts from the zygote and contains all cells up to a developmental stage with at least 100 cells. Third, all the terminal cells at this stage must be included in the lineage data. Fourth, the terminal cells should be functionally categorized because the impact of a cell death depends on the cell type. There are only three developmental cell lineages that meet all these criteria (C. elegans, P. marina, and H. roretzi) and they were retrieved from an earlier publication [26]. Several other well-known cell lineages do not satisfy one or more of the four requirements and thus cannot be used here (Table S2). In the C. elegans cell lineage, 671 terminal cells were categorized by standard anatomical descriptions [25] as: 39 blast, 113 death, 93 epithelial (arcade, hypodermis, pharyngeal structural, rectum, valves), 2 germ, 13 gland (coelomocytes, excretory system, and pharyngeal glands), 20 intestinal, 123 muscle (including the head mesodermal cell), 46 neural structural cells, and 222 neurons. To consider the potentially different importance of cells of the same type, we subdivided neurons into two excretory canal neurons, 95 interneurons, 45 motor neurons, 26 polymodal neurons, and 54 sensory neurons [26]. We also validated our primary result using an expanded post-embryonic hermaphroditic C. elegans cell lineage with a total of 937 terminal cells, including 5 blast, 131 death, 262 epithelial (arcade, hypodermis, pharyngeal structural, rectum, valves), 2 germ, 13 gland (coelomocytes, excretory system, and pharyngeal glands), 20 intestinal, 153 muscle (including the head mesodermal cell), 46 neural structural, and 305 neuronal cells [29], [64]. For P. marina, the cell lineage up to muscle contraction, containing 638 terminal cells, were classified as: 81 body muscle, 67 death, 2 germ, 131 hypodermis, 20 intestine, 195 nervous system, 112 pharynx, and 30 unknown fate [24]. For H. roretzi, the cell lineage up to the 110-cell stage was used. The terminal cells were classified according to the fates of their descendants [30] as: 12 endoderm, 50 epidermis, 6 mesenchyme (and trunk lateral cells), 10 muscle (and trunk ventral cells), 16 nervous system (brain, nerve cord, palps, primordial pharynx, and sensory pigment cells), 10 notochord, and 6 undifferentiated.
Estimation of fp
If the program failure rate is p, the number of programs that fail in a lineage is a random variable b following the binomial distribution B(Nprogram, p), where Nprogram is the total number of unique programs in the lineage. After randomly picking b failed programs, we calculated f using Eq. (1). The above step was repeated 10Nall times to calculate the expected f. Here Nall is the total number of cells in the lineage. We used p = 1/Ninternal, where Ninternal is the number of internal cells in the lineage. The above assumed relationship between p and Ninternal ensures that the expected number of internal cells whose division programs fail is the same between a real lineage and all of its randomized lineages, which is required for a fair comparison of their fp values. For two reasons, the stochasticity involved in the estimation of fp is unavoidable. First, despite the constancy in the expected number of cells with failed programs, the expected number of failed programs varies between a real lineage and its random lineages. Second, because b could be large, it is computationally impossible to explore all possibilities in the event of multiple program failures.
Generation of random cell lineages
We generated random lineages under eight different constraints. (i) We randomly coalesced the terminal cells of a real lineage (Figs. 1E–J) using the following procedure. Suppose there are m terminal cells. We randomly pick two of them (regardless of their cell types) and coalesce them, meaning that they become sisters and share the immediate progenitor cell. There are now m-1 cells left (m-2 terminal cells and 1 progenitor cell). We then randomly pick two cells from these m-1 cells and repeat the coalescence process until there is only one cell left. This process generates a random cell lineage of the m terminal cells (Fig. S2). (ii) We constrained the random coalescent process such that the maximum depth is fixed at a predetermined value (Figs. 2B–D). (iii) We constrained the random coalescent process such that the maximum depth is fixed at a predetermined value and the mean depth is close to a predetermined value (i.e., cell depths in a random lineage is a bootstrap sample of the real depths) (Figs. 2E, F). (iv) We generated random lineages by constraining the distribution of the depths of all terminal cells as in a real lineage but allowing variation of the lineage tree structure and depths of individual cells. In procedures (iii) and (iv), when the set of cell depths is given, each terminal cell is randomly assigned with one of the depths. We then randomly paired-up the xy cells at the maximum depth y as sister cells, creating xy/2 internal cells at depth y-1. It is repeated at depth y-1 for the (xy/2+xy-1) cells, and then recursively at depth y-2, y-3, …, and 1 (Figs. 3A, B). (v) We generated random lineages that have the same topology as a real lineage and then randomly shuffled all the terminal cells (Figs. 3C, D; Figs. 4B–D; Figs. 7A, B). (vi) We shuffled all the terminal cells in a real lineage within their respective depths (Figs. 5D, E; Figs. 7A, B). (vii) In addition to the constraint in (vi), we further maintained the twin terminal cells as twins in shuffling (Figs. 5D, E; Figs. 7A, B). (viii) We first defined a random order of cell types. Within each depth, g percent of terminal cells in every type are picked and sorted by the predefined type order, while the remaining unsorted cells are randomly inserted into the sorted list of cells. The cells are then assigned in the order of appearance in the list to the terminal nodes at that given depth from the left to the right of the lineage. The procedure is repeated for every depth (with the same cell type order) to create a lineage whose clonality increases with g (Figs. 5A–C, F). For all except the second and eighth constraints, we generated 10,000 random lineages. For the second constraint, we set the maximum depth as small as Dmin and as large as Dreal+2(Dreal−Dmin+1), where Dmin is the theoretical lower limit of the lineage's maximum depth and Dreal is the observed maximum depth of the real lineage. We then generated 5,000 random lineages for each possible maximum depth between these two extremes. For the eighth constraint, we used g at every 5th percentile, and created 50 random lineages for each value of g. The source codes for generating the random lineages can be downloaded from http://code.google.com/p/eadlin/downloads/list.
Terminal cell type classification based on single-cell gene expression data
Gene expression profiles of 93 genes in 363 cells at the C. elegans L1 stage [28] were retrieved. Three of the 363 cells are not terminal cells in the lineage considered here and are thus removed. We then used the hclust function in the R package to hierarchically cluster the 360 cells based on the pair-wise Euclidean distances in the expression levels of the 93 genes. The tree is cut at an appropriate height to acquire a designated number of groups of cells (e.g. cutting at the root will result in two groups); these groups are regarded as transcriptome-based cell types.
Constraints imposed by the spatial organization of terminal cells
The three-dimensional spatial coordinates of 334 terminal cells in the C. elegans lineage were retrieved from a recent paper [43]. The physical distance between two cells is the Euclidian distance between the centers of their nuclei [43]. To search for a cell lineage with ρp-l greater than that (0.2533) observed in C. elegans, we randomly generated 100 lineages that differ from the C. elegans lineage by only one swap between two terminal cells of the same depth and type. We chose the lineage with the highest ρp-l among the 100 random lineages, and repeated this process 100 times to obtain a lineage with ρp-l = 0.4085 (the square in Fig. 5C).
Using terminal cells with three-dimensional coordinates, we calculated the mean physical distance between a pair of twin cells in C. elegans. We similarly calculated the mean physical distance between a pair of randomly picked terminal cells of the same type for the same number of pairs as twins. We repeated this calculation 100 times to estimate the mean and standard deviation. These values allowed the calculation of a Z-score for the observed value from the twins.
Simulation of macroevolution of developmental cell lineages
The macroevolution simulation is designed to mimic the evolutionary expansion of a cell lineage under the constraint of its ancestral forms. Basically, the evolution is modeled by repeated additions of terminal cells, and each individual addition is called a round of bifurcation. To ensure that the macroevolution generates a cell lineage that is comparable to a given real lineage, we first completely shuffled the terminal cells of the real lineage to obtain a randomized terminal cell sequence. Starting from the first cell in the sequence as the founder cell, a lineage of m terminal cells is evolved by m-1 rounds of bifurcation. In each round, one random terminal cell from the evolved lineage is chosen and divided into two daughter cells. After the division, one of the daughter cells inherits the cell type of its parental cell, whereas the other is assigned the type of the next cell in the predetermined terminal cell sequence. The parental cell then becomes an internal cell with a division program generating its original cell type and the new cell type. At each step of lineage expansion, 100 random bifurcations are examined. Among them, a random lineage is chosen from the top k robust lineages as the starter of the next round of expansion, where k is adjusted between 1 and 100 to represent different selection intensities. The smaller the k value, the stronger the selection. In Fig. 6 and Fig. S7, the presented selection intensity equals k/100; in Fig. 7 and Fig. S8, k equals 5. Regardless of the cell lineage size, we used an expected necrosis rate of 1 necrosis per cell lineage or an expected program failure rate of 1/Ninternal failure per program. For the macroevolution involving selection for simplicity S ( = 1/complexity), we calculated lineage complexity [26] at every round of bifurcation and combined it with the robustness (R) to define the fitness of a lineage. For instance, R5S (Fig. 7B) means that fitness = R5S. Here R equals fn defined in Eq. (1). Under each parameter set, we repeated the macroevolution 100 times to access variations. For the developmental cell lineage of H. roretzi, to retain its fully symmetric feature during macroevolution, bifurcations were carried out in one half of the lineage, but the robustness was calculated after mirroring the half lineage. The source code of the macroevolution simulation can be downloaded from http://code.google.com/p/eadlin/downloads/list.
Loss of terminal cells distributed among several cell types versus one type
Based on Eq. (1), it is clear that when different cell types have different numbers of (terminal) cells, a cell death that happens to a common cell type would have a smaller effect on f than a cell death that happens to a rare cell type. Now let us consider the scenario of T terminal cell types, each with exactly N terminal cells. Let h terminal cells to die, where 1<h<N. If all dead cells are of the same type, we have . If we arbitrarily assign h1 (0<h1<h) cell death events to another cell type, we have . It can be shown that . Assigning h1 cell deaths to a second type and h2 cell deaths to a third type (0<h2<h-h1) would result in . It can also be shown that . The same is true when the cell deaths are distributed among more cell types. Thus, the loss of multiple terminal cells of the same type tends to result in a lower f than the loss of the same number of terminal cells distributed among several types.
Supporting Information
Zdroje
1. WaddingtonCH (1942) Canalization of development and the inheritance of acquired characters. Nature 150 : 563–565.
2. MaselJ, SiegalML (2009) Robustness: mechanisms and consequences. Trends Genet 25 : 395–403.
3. FlattT (2005) The evolutionary genetics of canalization. Q Rev Biol 80 : 287–316.
4. ScharlooW (1991) Canalization: genetic and developmental aspects. Annu Rev Ecol Syst 22 : 65–93.
5. Wagner A (2005) Robustness and Evolvability in Living Systems. Princeton, NJ: Princeton University Press.
6. Alon U (2007) An Introduction to Systems Biology: Design Principles of Biological Circuits London: Chapman & Hall.
7. HoWC, ZhangJ (2014) The genotype-phenotype map of yeast complex traits: basic parameters and the role of natural selection. Mol Biol Evol 31(6): 1568–80.
8. DraghiJA, ParsonsTL, WagnerGP, PlotkinJB (2010) Mutational robustness can facilitate adaptation. Nature 463 : 353–355.
9. LevySF, SiegalML (2008) Network hubs buffer environmental variation in Saccharomyces cerevisiae. PLoS Biol 6: e264.
10. RutherfordSL, LindquistS (1998) Hsp90 as a capacitor for morphological evolution. Nature 396 : 336–342.
11. Zhang J (2012) Genetic redundancies and their evolutionary maintenance. In: Soyer O, editor. Evolutionary Systems Biology. New York, NY: Springer.
12. WangZ, ZhangJ (2009) Abundant indispensable redundancies in cellular metabolic networks. Genome Biol Evol 1 : 23–33.
13. NowakMA, BoerlijstMC, CookeJ, SmithJM (1997) Evolution of genetic redundancy. Nature 388 : 167–171.
14. QianW, LiaoBY, ChangAY, ZhangJ (2010) Maintenance of duplicate genes and their functional redundancy by reduced expression. Trends Genet 26 : 425–430.
15. VavouriT, SempleJI, LehnerB (2008) Widespread conservation of genetic redundancy during a billion years of eukaryotic evolution. Trends Genet 24 : 485–488.
16. SiegalML, BergmanA (2002) Waddington's canalization revisited: developmental stability and evolution. Proc Natl Acad Sci U S A 99 : 10528–10532.
17. HornsteinE, ShomronN (2006) Canalization of development by microRNAs. Nat Genet 38 Suppl: S20–24.
18. WuCI, ShenY, TangT (2009) Evolution under canalization and the dual roles of microRNAs: a hypothesis. Genome Res 19 : 734–743.
19. PrillRJ, IglesiasPA, LevchenkoA (2005) Dynamic properties of network motifs contribute to biological network organization. PLoS Biol 3: e343.
20. Gilbert SF (2000) Developmental Biology. Sunderland, Mass.: Sinauer Associates.
21. DictusWJ, DamenP (1997) Cell-lineage and clonal-contribution map of the trochophore larva of Patella vulgata (mollusca). Mech Dev 62 : 213–226.
22. LambertJD (2010) Developmental patterns in spiralian embryos. Curr Biol 20: R72–77.
23. NodaT, HamadaM, HamaguchiM, FujieM, SatohN (2009) Early zygotic expression of transcription factors and signal molecules in fully dissociated embryonic cells of Ciona intestinalis: A microarray analysis. Dev Growth Differ 51 : 639–655.
24. HouthoofdW, JacobsenK, MertensC, VangestelS, CoomansA, et al. (2003) Embryonic cell lineage of the marine nematode Pellioditis marina. Dev Biol 258 : 57–69.
25. SulstonJE, SchierenbergE, WhiteJG, ThomsonJN (1983) The embryonic cell lineage of the nematode Caenorhabditis elegans. Dev Biol 100 : 64–119.
26. AzevedoRB, LohausR, BraunV, GumbelM, UmamaheshwarM, et al. (2005) The simplicity of metazoan cell lineages. Nature 433 : 152–156.
27. VlachosM, TavernarakisN (2010) Non-apoptotic cell death in Caenorhabditis elegans. Dev Dyn 239 : 1337–1351.
28. LiuX, LongF, PengH, AerniSJ, JiangM, et al. (2009) Analysis of cell fate from single-cell gene expression profiles in C. elegans. Cell 139 : 623–633.
29. Altun ZF, Herndon L.A., Crocker C., Lints R. and Hall D.H. (2010) WormAtlas. http://www.wormatlas.org/.
30. NishidaH (1987) Cell lineage analysis in ascidian embryos by intracellular injection of a tracer enzyme. III. Up to the tissue restricted stage. Dev Biol 121 : 526–541.
31. AveryL, HorvitzHR (1987) A cell that dies during wild-type C. elegans development can function as a neuron in a ced-3 mutant. Cell 51 : 1071–1078.
32. StentGS (1998) Developmental cell lineage. Int J Dev Biol 42 : 237–241.
33. Slack JMW (1983) From Egg to Embryo. Cambridge: Cambridge University Press
34. LawsonKA, MenesesJJ, PedersenRA (1991) Clonal analysis of epiblast fate during germ layer formation in the mouse embryo. Development 113 : 891–911.
35. HeldeKA, WilsonET, CretekosCJ, GrunwaldDJ (1994) Contribution of early cells to the fate map of the zebrafish gastrula. Science 265 : 517–520.
36. DormannD, WeijerCJ (2006) Imaging of cell migration. EMBO J 25 : 3480–3493.
37. ZamirEA, CzirokA, CuiC, LittleCD, RongishBJ (2006) Mesodermal cell displacements during avian gastrulation are due to both individual cell-autonomous and convective tissue movements. Proc Natl Acad Sci U S A 103 : 19806–19811.
38. WasserstromA, AdarR, SheferG, FrumkinD, ItzkovitzS, et al. (2008) Reconstruction of cell lineage trees in mice. PLoS One 3: e1939.
39. SalipanteSJ, KasA, McMonagleE, HorwitzMS (2010) Phylogenetic analysis of developmental and postnatal mouse cell lineages. Evol Dev 12 : 84–94.
40. ReizelY, ItzkovitzS, AdarR, ElbazJ, JinichA, et al. (2012) Cell lineage analysis of the mammalian female germline. PLoS Genet 8: e1002477.
41. KimmelCB, WargaRM, SchillingTF (1990) Origin and organization of the zebrafish fate map. Development 108 : 581–594.
42. StentGS (1985) The role of cell lineage in development. Philos Trans R Soc Lond B Biol Sci 312 : 3–19.
43. LongF, PengH, LiuX, KimSK, MyersE (2009) A 3D digital atlas of C. elegans and its application to single-cell analyses. Nat Methods 6 : 667–672.
44. FelixMA, BarkoulasM (2012) Robustness and flexibility in nematode vulva development. Trends Genet 28 : 185–195.
45. ShostakS (2008) Speculation on the evolution of stem cells. Breast Dis 29 : 3–13.
46. ZhangJ, JeradiS, StrahleU, AkimenkoMA (2012) Laser ablation of the sonic hedgehog-a-expressing cells during fin regeneration affects ray branching morphogenesis. Dev Biol 365 : 424–433.
47. WangZ, ZhangJ (2011) Impact of gene expression noise on organismal fitness and the efficacy of natural selection. Proc Natl Acad Sci U S A 108: E67–76.
48. WagnerG, BoothG, Bagheri-ChaichianH (1997) A population genetic theory of canalization. Evolution 51 : 329–347.
49. LohausR, GeardNL, WilesJ, AzevedoRB (2007) A generative bias towards average complexity in artificial cell lineages. Proc Biol Sci 274 : 1741–1750.
50. ItzkovitzS, BlatIC, JacksT, CleversH, van OudenaardenA (2012) Optimality in the development of intestinal crypts. Cell 148 : 608–619.
51. HouthoofdW, WillemsM, JacobsenK, CoomansA, BorgonieG (2008) The embryonic cell lineage of the nematode Rhabditophanes sp. Int J Dev Biol 52 : 963–967.
52. HouthoofdW, BorgonieG (2007) The embryonic cell lineage of the nematode Halicephalobus gingivalis (Nematoda: Cephalobina: Panagrolaimoidea). Nematology 9 : 573–584.
53. GaoJJ, PanXR, HuJ, MaL, WuJM, et al. (2011) Highly variable recessive lethal or nearly lethal mutation rates during germ-line development of male Drosophila melanogaster. Proc Natl Acad Sci U S A 108 : 15914–15919.
54. EllisHM, HorvitzHR (1986) Genetic control of programmed cell death in the nematode C. elegans. Cell 44 : 817–829.
55. Starz-GaianoM, LehmannR (2001) Moving towards the next generation. Mech Dev 105 : 5–18.
56. McLarenA (2003) Primordial germ cells in the mouse. Dev Biol 262 : 1–15.
57. KellySJ (1977) Studies of the developmental potential of 4 - and 8-cell stage mouse blastomeres. J Exp Zool 200 : 365–376.
58. CarlsonCA, KasA, KirkwoodR, HaysLE, PrestonBD, et al. (2012) Decoding cell lineage from acquired mutations using arbitrary deep sequencing. Nat Methods 9 : 78–80.
59. ZongC, LuS, ChapmanAR, XieXS (2012) Genome-wide detection of single-nucleotide and copy-number variations of a single human cell. Science 338 : 1622–1626.
60. HouY, SongL, ZhuP, ZhangB, TaoY, et al. (2012) Single-cell exome sequencing and monoclonal evolution of a JAK2-negative myeloproliferative neoplasm. Cell 148 : 873–885.
61. XuX, HouY, YinX, BaoL, TangA, et al. (2012) Single-cell exome sequencing reveals single-nucleotide mutation characteristics of a kidney tumor. Cell 148 : 886–895.
62. SalipanteSJ, HorwitzMS (2006) Phylogenetic fate mapping. Proc Natl Acad Sci U S A 103 : 5448–5453.
63. FrumkinD, WasserstromA, KaplanS, FeigeU, ShapiroE (2005) Genomic variability within an organism exposes its cell lineage tree. PLoS Comput Biol 1: e50.
64. SulstonJE, HorvitzHR (1977) Post-embryonic cell lineages of the nematode, Caenorhabditis elegans. Dev Biol 56 : 110–156.
Štítky
Genetika Reprodukční medicínaČlánek vyšel v časopise
PLOS Genetics
2014 Číslo 7
Nejčtenější v tomto čísle
- Wnt Signaling Interacts with Bmp and Edn1 to Regulate Dorsal-Ventral Patterning and Growth of the Craniofacial Skeleton
- Novel Approach Identifies SNPs in and with Evidence for Parent-of-Origin Effect on Body Mass Index
- Hypoxia Adaptations in the Grey Wolf () from Qinghai-Tibet Plateau
- DNA Topoisomerase 1α Promotes Transcriptional Silencing of Transposable Elements through DNA Methylation and Histone Lysine 9 Dimethylation in
Zvyšte si kvalifikaci online z pohodlí domova
Současné možnosti léčby obezity
nový kurzVšechny kurzy


