-
Články
Top novinky
Reklama- Vzdělávání
- Časopisy
Top články
Nové číslo
- Témata
Top novinky
Reklama- Videa
- Podcasty
Nové podcasty
Reklama- Kariéra
Doporučené pozice
Reklama- Praxe
Top novinky
ReklamaSex-Differential Selection and the Evolution of X Inactivation Strategies
X inactivation—the transcriptional silencing of one X chromosome copy per female somatic cell—is universal among therian mammals, yet the choice of which X to silence exhibits considerable variation among species. X inactivation strategies can range from strict paternally inherited X inactivation (PXI), which renders females haploid for all maternally inherited alleles, to unbiased random X inactivation (RXI), which equalizes expression of maternally and paternally inherited alleles in each female tissue. However, the underlying evolutionary processes that might account for this observed diversity of X inactivation strategies remain unclear. We present a theoretical population genetic analysis of X inactivation evolution and specifically consider how conditions of dominance, linkage, recombination, and sex-differential selection each influence evolutionary trajectories of X inactivation. The results indicate that a single, critical interaction between allelic dominance and sex-differential selection can select for a broad and continuous range of X inactivation strategies, including unequal rates of inactivation between maternally and paternally inherited X chromosomes. RXI is favored over complete PXI as long as alleles deleterious to female fitness are sufficiently recessive, and the criteria for RXI evolution is considerably more restrictive when fitness variation is sexually antagonistic (i.e., alleles deleterious to females are beneficial to males) relative to variation that is deleterious to both sexes. Evolutionary transitions from PXI to RXI also generally increase mean relative female fitness at the expense of decreased male fitness. These results provide a theoretical framework for predicting and interpreting the evolution of chromosome-wide expression of X-linked genes and lead to several useful predictions that could motivate future studies of allele-specific gene expression variation.
Published in the journal: . PLoS Genet 9(4): e32767. doi:10.1371/journal.pgen.1003440
Category: Research Article
doi: https://doi.org/10.1371/journal.pgen.1003440Summary
X inactivation—the transcriptional silencing of one X chromosome copy per female somatic cell—is universal among therian mammals, yet the choice of which X to silence exhibits considerable variation among species. X inactivation strategies can range from strict paternally inherited X inactivation (PXI), which renders females haploid for all maternally inherited alleles, to unbiased random X inactivation (RXI), which equalizes expression of maternally and paternally inherited alleles in each female tissue. However, the underlying evolutionary processes that might account for this observed diversity of X inactivation strategies remain unclear. We present a theoretical population genetic analysis of X inactivation evolution and specifically consider how conditions of dominance, linkage, recombination, and sex-differential selection each influence evolutionary trajectories of X inactivation. The results indicate that a single, critical interaction between allelic dominance and sex-differential selection can select for a broad and continuous range of X inactivation strategies, including unequal rates of inactivation between maternally and paternally inherited X chromosomes. RXI is favored over complete PXI as long as alleles deleterious to female fitness are sufficiently recessive, and the criteria for RXI evolution is considerably more restrictive when fitness variation is sexually antagonistic (i.e., alleles deleterious to females are beneficial to males) relative to variation that is deleterious to both sexes. Evolutionary transitions from PXI to RXI also generally increase mean relative female fitness at the expense of decreased male fitness. These results provide a theoretical framework for predicting and interpreting the evolution of chromosome-wide expression of X-linked genes and lead to several useful predictions that could motivate future studies of allele-specific gene expression variation.
Introduction
Mammalian females transcriptionally silence one of their two X chromosomes within each somatic cell – a process called X inactivation [1], [2]. The basic phenomenon of X inactivation occurs in all therian (non egg-laying) mammals studied to date, yet the specific X chromosome silenced exhibits considerable diversity among species. At one extreme, typical of marsupials, the paternally inherited X is universally silenced and the maternally inherited X is ubiquitously expressed ([3], [4]; hereafter referred to as paternal X inactivation or PXI). In contrast, placental mammals practice random X inactivation (RXI): each somatic cell may express either the maternally or the paternally inherited X (the other X is silenced), and female bodies are composed of a mosaic of cells that individually express one of the two X chromosome copies [5]. While RXI is generally thought to be unbiased – with each cell having an equal probability of expressing either of the two X chromosomes – recent data reveal quantitatively biased inactivation patterns in at least some placental mammal species, i.e.: differential silencing of maternally and paternally derived X chromosomes [6], [7]. Several marsupial studies similarly find evidence for partial expression of the paternally derived X, suggesting additional species-specificity of X inactivation rules (reviewed in [2], [8]).
The selective processes that might account for this observed diversity remain unclear. A leading hypothesis for the evolution of RXI is that it might be favored if segregating deleterious mutations have recessive or partially recessive fitness effects ([9]–[11]; which, on average, they do [12]–[15]). The logic underlying this hypothesis is straightforward. Females that uniformly silence a particular copy of the X (e.g., the paternally inherited copy under PXI) will be effectively haploid, and suffer the full fitness costs of mutations carried on their expressed X chromosome. RXI generates an expression pattern that is more similar to diploidy, and can potentially mask the fitness costs of carrying deleterious alleles.
While the masking hypothesis for the evolutionary origins of RXI is plausible (e.g., [1], [16]–[20]), its feasibility should be investigated in a formal population genetic model. Models of a similar evolutionary scenario, the evolution of haploid versus diploid life cycles (e.g., [21]–[25]), indicate that selection for masking of deleterious mutations favors the evolution of diploidy, if mutations are sufficiently recessive relative to the population's recombination rate ([26]–[30]; however, selection to mask somatic mutations eliminates constraints imposed by tight linkage [31]). However, these models do not incorporate the unique properties of sex-differential selection and inheritance that govern X chromosome evolution [32], so it remains unclear whether their conclusions apply to the case of RXI.
Sex differences in selection – where the fitness effects of single mutations differ in magnitude or direction between males and females – likely influence large fractions of animal genomes [33]–[36], which can have two potential consequences for the evolutionary diversification of X inactivation strategies. Stronger selection against deleterious alleles in males compared to females should decrease the average proportion of deleterious alleles carried on each paternally derived X (e.g., [10], [33]), and thereby favor expressing the paternally inherited X. “Sexually antagonistic alleles” – alleles that increase fitness when present in one sex, but decrease fitness in the other sex [37], [38] – should have the opposite effect on X inactivation. Alleles benefiting males and costly to females experience higher probabilities of paternal transmission (e.g., [39], [40]), which could generate selection to preferentially inactivate, or even ubiquitously silence, paternally inherited X chromosomes. Several models have examined how sexually antagonistic selection might favor the evolution genomic imprinting, which similarly involves the unequal expression of maternally and paternally inherited gene copies [40]–[44]. However, the effect of sexually antagonistic fitness variation on X inactivation evolution has yet to be addressed.
It is currently unclear how the population genetic parameters of dominance, sex-differential selection, and linkage and recombination might jointly influence the evolution of X inactivation strategies. We therefore developed a mathematical model of X inactivation evolution, and used this model to identify biological conditions that favor the evolution of different X inactivation states. We first consider the dichotomous case of RXI versus PXI, describe the conditions facilitating evolutionary transitions to RXI, and characterize the consequences of such transitions for mean fitness of males and females. Overall, selection on mammalian X inactivation strategies is primarily mediated by the interaction between dominance and sex-differential selection, and the situation differs considerably from scenarios that favor the evolution of diploidy. We also examine whether sex-differential selection might favor the evolution of biased X inactivation strategies (i.e., quantitatively unequal expression of maternally versus paternally derived X chromosomes) and predict the magnitude of biases likely to evolve. Our results suggest that conditions for evolving biased inactivation patterns are extremely permissive.
Results
Development of the model
We focus on the simplest and most analytically tractable model that simultaneously incorporates genetic linkage, variation for fitness, and variation in the form of X inactivation. Our model follows the evolution of two bi-allelic loci. Locus A (the “fitness locus”) is X-linked and carries A1 and A2 alleles, which directly influence male and female fitness. Locus B (the “modifier locus”) carries B1 and B2 alleles, which influence the X inactivation rule in females within the population. The genotype at locus B can influence female fitness through its effect on the relative expression of A1 versus A2 alleles in heterozygotes. Variation at the B locus has no other phenotypic effect in males or females and is therefore neutral in males. We consider two scenarios of linkage for the B locus. Under X-linkage, A and B are physically linked, and recombine at a rate r, per female meiosis (the X does not recombine in males, which have only one X chromosome copy). When B is on an autosome, alleles at A and B loci segregate independently during meiosis.
To model the evolution of X inactivation, we begin with the B locus initially fixed for allele B1, and the A locus at polymorphic equilibrium given B1 fixed. We then characterize selection on and evolution of a novel B2 allele that changes a female carrier's X inactivation system. The population is assumed to be sufficiently large that genetic drift can be ignored, and each generation is discrete. The life cycle during each generation follows the order of birth, selection, recombination, mutation, random mating and syngamy. Our approach bears many similarities to models for the evolution of ploidy cycles (e.g., [26], [45] chapter 8 of [46]), and for the evolution of sexually dimorphic genomic imprinting [40], [44], with which we draw contrasts. Generalized two-locus recursions (see Methods) include sixteen different female genotypes (when allowing for parent-of-origin effects) and at least four male genotypes (four for the X-linked modifier model; eight for the autosomal modifier model). To reduce the enormous range of possible fitness parameterizations and initial population conditions, we focus our attention on a subset of idealized and biologically relevant population genetic scenarios in the following analyses.
We consider two basic forms of fitness variation at the A locus (Table 1): (1) deleterious alleles maintained at a balance between recurrent mutation and purifying selection; and (2) sexually antagonistic alleles stably maintained as balanced polymorphisms. In both scenarios, the female-deleterious allele is denoted by A1, i.e. female fitness is highest in A2 homozygotes, and fitness of heterozygous females is assumed to be intermediate to the two homozygous genotypes [formally, w(A1A1) = 1−sf≤w(A1A2), w(A2A1)≤w(A2A2) = 1, where w(AiAj) is the fitness of a female with genotype AiAj, and sf describes the fitness cost to females of being homozygous or haploid for the A1 allele: 1>sf>0]. When A1 is also deleterious to males, it will be maintained at mutation-selection balance (sm is the fitness cost to males of carrying an A1 allele; 1>sm>0; Table 1). We also consider genetic polymorphism maintained by sexual antagonism, where A2 is the deleterious allele for males (here, tm is the fitness cost to males of carrying an A2 allele; 1>tm>0; see Table 1).
Tab. 1. Fitnesses and frequencies of genotypes at the A locus.1 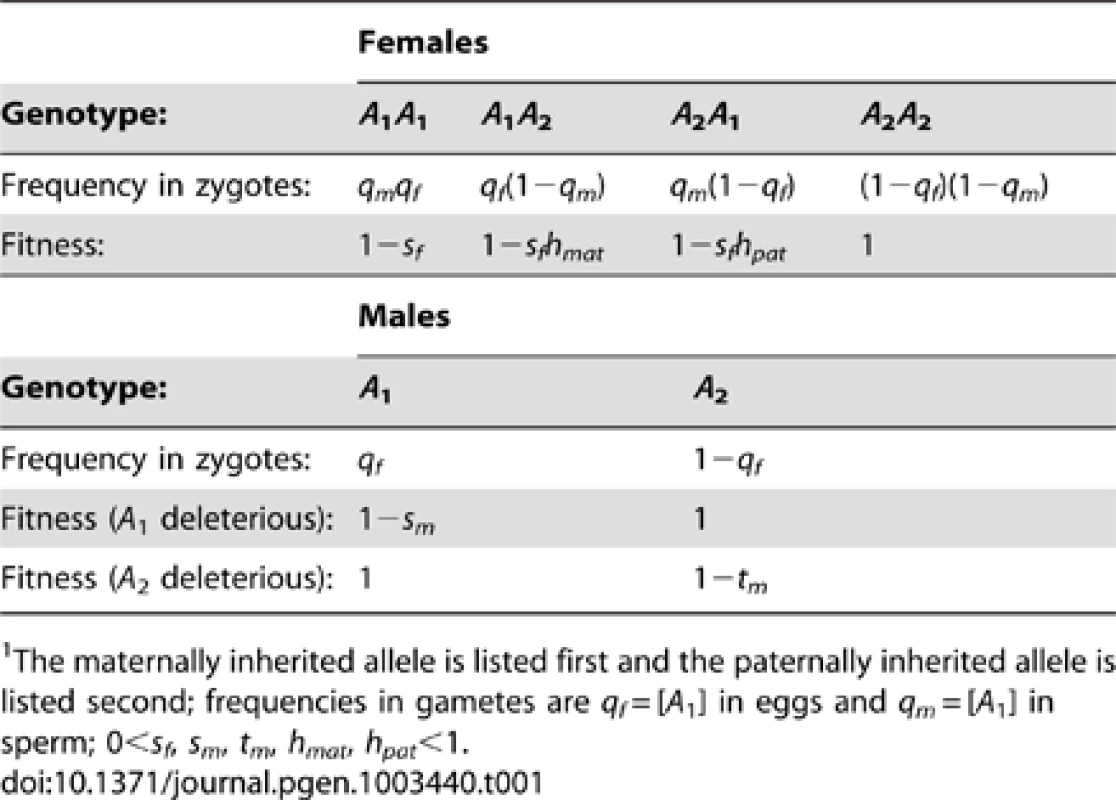
The maternally inherited allele is listed first and the paternally inherited allele is listed second; frequencies in gametes are qf = [A1] in eggs and qm = [A1] in sperm; 0<sf, sm, tm, hmat, hpat<1. In an ancestral population fixed for B1, female somatic cell lineages are assumed to silence the paternally inherited X with probability ξ11 and silence the maternal X with probability 1−ξ11 (0≤ξ11≤1). Under unbiased RXI (where ξ11 = ½), heterozygous females have fitness w(A1A2) = w(A2A1) = 1−sfh, where h represents the degree of masking of the A1 allele (0<h<1). Thus, h is a scaling factor that is analogous to the dominance coefficient of standard population genetic models. Use of the terms “dominance” and “recessivity”, applied to species with RXI, has been questioned because individual cells lack bi-allelic expression [47]. However, the dominance coefficient remains useful as a population genetic parameter, and simply quantifies the relative fitness of heterozygous versus homozygous genotypes when heterozygotes practice an unbiased RXI rule. Partial masking is clearly relevant for many X-linked disorders, which tend to be less penetrant and less severe in females than males [47].
When X inactivation is biased (ξ11≠½), fitness is function of h (as defined above) and parent-of-origin effects generated by the X inactivation rule. Assuming that female fitness decreases monotonically with the proportion of cells expressing the A1 allele, we can describe it using a generalized power function, w(x) = 1−xksf, where x represents the proportion of cells expressing the A1 allele, and k is a positive constant that describes the specific shape of the fitness decline associated with A1 expression (such functions are often used in evolutionary theory because of their flexibility; e.g., [48]–[50]). For our purposes, w(x) has two essential properties. First, fitness approaches unity when A2 is ubiquitously expressed (i.e., ), and 1−sf when A1 is ubiquitously expressed (i.e., ), which makes intuitive sense. Second, k can be defined in terms of the dominance coefficient of A1. When ξ11 = ½, x = ξ11 = 1−ξ11; therefore, h = 1/2k and k = −ln(h)/ln(2). A1 is partially dominant to A2 when h>½ (k<1) and partially recessive when h<½ (k>1). Consequently, hmat = ξ11k represents the effective dominance coefficient when A1 is maternally inherited, and hpat = (1−ξ11)k represents the effective dominance coefficient when A1 is paternally inherited (Table 1; Figure 1). Nonadditivity of allelic effects (i.e., h≠½) can arise when the fitness of an X-linked genotype is not cell-autonomous (e.g., fitness depends on the overall proportion of A1 versus A2 expression in female bodies; [43], [51]). With cell-autonomous effects, we can model total fitness as the mean fitness per cell [43], such that w(A1A2) = 1−ξ11sf and w(A2A1) = 1−(1−ξ11)sf, which represents a special case of the generalized power function (i.e., k = 1 and h = ½).
Fig. 1. Relationship between X inactivation rule and parent-of-origin dominance coefficients (hmat, hpat; see Table 1). 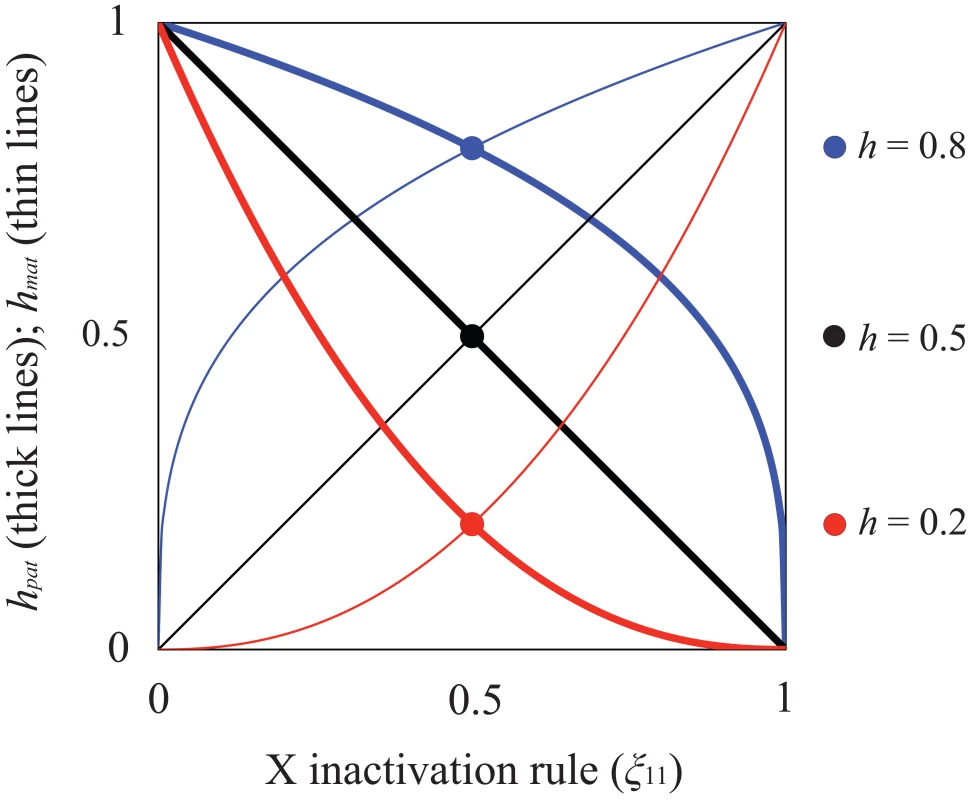
Results are based on the power function for female fitness, w(x) = 1−xksf, where x represents the proportion of female cells expressing the A1 allele, sf is the haploid or homozygous selection coefficient, h is the degree of masking (equivalent to a dominance coefficient of A1) in individuals practicing unbiased RXI (ξ11 = ½), and k = −ln(2)/ln(h). For additional details, see the main text. The figure is modified from, and inspired by, Figure 1a of [50]. Given the outlined assumptions, we obtain the following equilibria with respect to the X-linked fitness-determining locus. When A1 is deleterious to both sexes, its equilibrium frequencies at mutation-selection balance (in females and males, respectively) are:
where u is the mutation rate to A1, hmat = ξ11k, and hpat = (1−ξ11)k, and k = −ln(h)/ln(2). Eq. (1) was previously derived in [52] (see Text S1). When A1 is sexually antagonistic (i.e., deleterious to females but beneficial to males), and with balancing selection acting at the A locus, the equilibrium frequencies of A1 are: versions of which have been derived in several previous studies [43], [52]–[54]. The balancing selection criteria for sexually antagonistic polymorphism are provided (Text S1; for additional results and discussion, see [43], [52], [54]–[56]).Evolution of random X inactivation
PXI is thought to represent the ancestral X inactivation state, from which RXI evolved [1], [57]. We therefore sought to define the population genetic conditions in which a rare B2 allele that causes unbiased RXI (where ξ12 = ½ represents the X inactivation strategy played by individuals heterozygous at the modifier locus) will invade a population that is initially fixed for the PXI strategy (ξ11 = 1).
Mutation-selection balance
To examine whether segregating recessive deleterious mutations might be sufficiently masked by RXI to render such a strategy favorable to PXI ([10], [11]; see above), we performed a linear stability analysis using our general recursions (see Methods), and evaluated at the equilibrium with B1 fixed in the population and A1 at mutation-selection balance. As predicted, selection favors invasion of a modifier allele (B2) causing RXI when the deleterious allele is sufficiently masked in heterozygotes (i.e., h is sufficiently small). Assuming weak mutation at locus A (0<u≪1), the critical dominance coefficient under RXI is approximately:
Selection favors the evolution of RXI when h<hcrit (Figure 2). Note that Eq. (3) is independent of the recombination rate between the A and B loci. This result applies equally to scenarios of X and autosomal linkage of the modifier locus.Fig. 2. Criteria for the evolution of RXI. 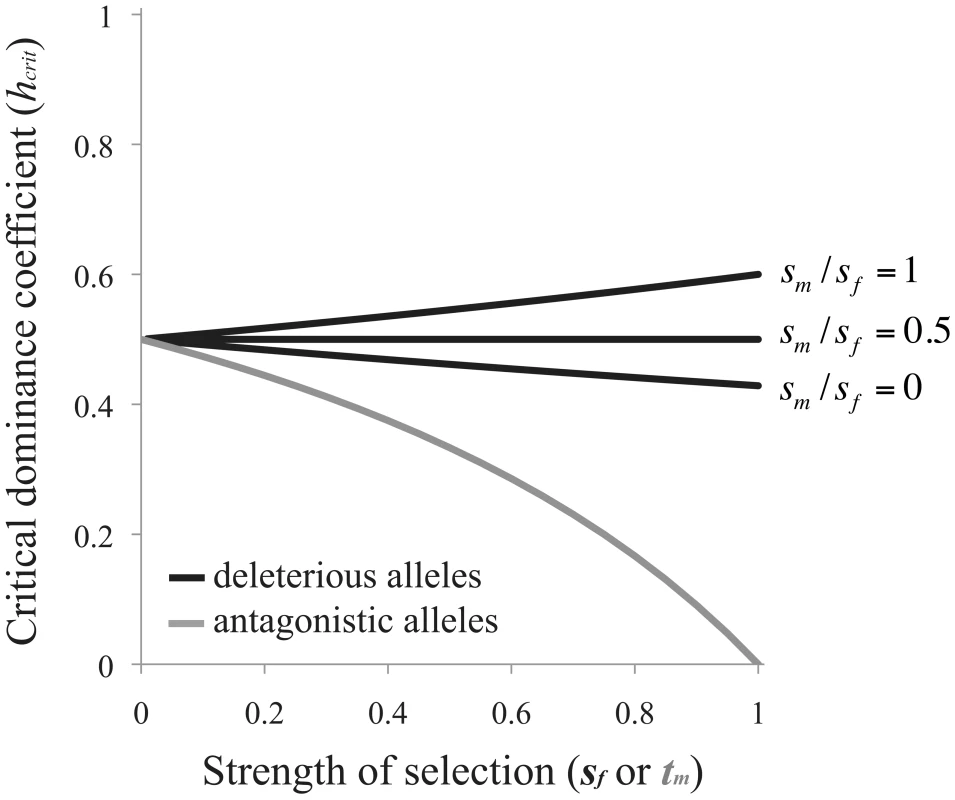
Black curves are based on eq. (3) for the mutation-selection balance model of genetic variation (in which case, the x-axis refers to the female selection coefficient, sf). The gray curve is based on eq. (4) for sexually antagonistic alleles maintained by balancing selection (here, the x-axis refers to the male selection coefficient: tm). The area above each curve represents parameter space where unbiased RXI is not favored over PXI. RXI is favored under the complementary parameter space below each curve. When selection is weak (sm, sf→0), deleterious alleles need only be partially masked (h<½) for RXI to be favored. Increasing the strength of purifying selection alters hcrit, with stronger selection in males than females (large sm/sf ratios) expanding the parameter space in which RXI evolves, and female-biased selection decreasing it (small sm/sf ratios). This effect of differing selection strengths between the sexes has two contributing causes. First, expression of the paternally inherited X (as opposed to the maternal X) is favored because the frequency of deleterious mutations is lower on the paternal X. Second, purifying selection, primarily in males, limits the buildup of linkage disequilibrium (LD) between B2 alleles and deleterious mutations, which can also prevent the invasion of B2 alleles. This LD is generated from the epistatic interaction for female fitness between A and B locus genotypes, and there is no such epistasis in males. Limited evolution of LD expands the parameter space of dominance that permits the evolution of RXI.
Sexually antagonistic variation
Sexually antagonistic variation for fitness or its components has been detected in a variety of natural and experimental populations (e.g., [58]–[66]). Sexually antagonistic alleles polymorphic at an X-linked locus could potentially exert selection on X inactivation strategies. Our linear stability analysis of a population fixed for B1, with a deterministic balanced polymorphism for male-beneficial and female-deleterious alleles (eq. (2), with ξ11 = 1), shows that RXI will evolve when the dominance coefficient for the female-deleterious allele falls below the following threshold:
which is again independent of the linkage relationships between loci. Under weak selection (tm→0), female-detrimental alleles need only be partially masked for RXI to be favored, but overall, the conditions are considerably more restrictive than the mutation-selection balance model. Strong sexually antagonistic selection severely reduces the parameter space that favors the evolution of RXI (Figure 2). Thus, RXI can be selected against, despite strong effects of masking female-detriment alleles. This occurs when strong selection in males causes male-benefit/female-deleterious alleles to be disproportionately transmitted by male gametes.Changes in mean fitness when RXI evolves
Evolutionary transitions that influence gene ploidy levels (e.g., transitions from haploidy to diploidy) permit deleterious mutations to accumulate within populations, and reduce long-term population fitness (i.e., the new equilibrium fitness [21], [67]; however, epistasis can sometimes render diploidy advantageous [23]), which is why recombination is required for diploidy to evolve [26]–[30]. Under tight linkage, alleles for diploidy are co-transmitted with deleterious mutations, and fitness benefits of masking can be outweighed by the increased burden of linked, deleterious mutations. Recombination decouples such associations, and permits diploidy to evolve, despite the long-term fitness cost. Such interactions between ploidy and recombination have parallels in various other aspects of genome evolution, including the evolution of genomic imprinting [44], [68] and the establishment of gene duplicates [69], [70].
In contrast, the evolution of RXI does not require recombination (as shown above), and this insensitivity to linkage can similarly be considered in light of mean fitness changes that follow an evolutionary transition from PXI to RXI. For the mutation-selection balance model, equilibrium mean male and female fitnesses (respectively) under PXI and unbiased RXI are:
and which each ignore terms of O(u2). For the parameter space where RXI can evolve [h<3/(6−2sm+sf); see eq. (3)], mean male fitness is always lower under RXI (as long as sm>0; otherwise fitness does not change). Mean female fitness becomes higher, as the evolution of RXI shifts some of the burden of purifying selection (removing deleterious mutations) from females to males. The fitness cost to males at the new equilibrium is offset by fitness gains to females, which provides an intuitive explanation as to why selection for RXI is insensitive to linkage. Tightly linked deleterious alleles may hitchhike with a modifier for RXI, yet such associations do not overturn the net benefits of masking.For the case of an evolutionary transition from PXI to RXI driven by sexually antagonistic polymorphism [in the parameter space where RXI can evolve, i.e.: h<(1−tm)/(2−tm); see eq. (4)], the new equilibrium frequency of the male-beneficial/female-detrimental allele will be higher when tm<sf, and lower when tm>sf. Mean male fitness is therefore increased after the transition when sf>tm, decreased when sf<tm, and otherwise remains unchanged. The mean female fitness is increased under a much broader range of conditions, because the masking effect caused by RXI can sometimes offset a higher derived frequency of the female-deleterious allele. The condition necessary for female fitness to be increased following the evolution of RXI is:
where hcrit = (1−tm)/(2−tm). As shown in Figure 3, parameter conditions favoring the evolution of RXI generally lead to an increase in mean female fitness, whereas mean male fitness is increased in exactly half of the relevant parameter space. The new mean fitness is always increased in one sex at least, and in some cases, in both sexes.Fig. 3. Sexually antagonistic fitness variation and the change in mean fitness following the evolution of RXI. 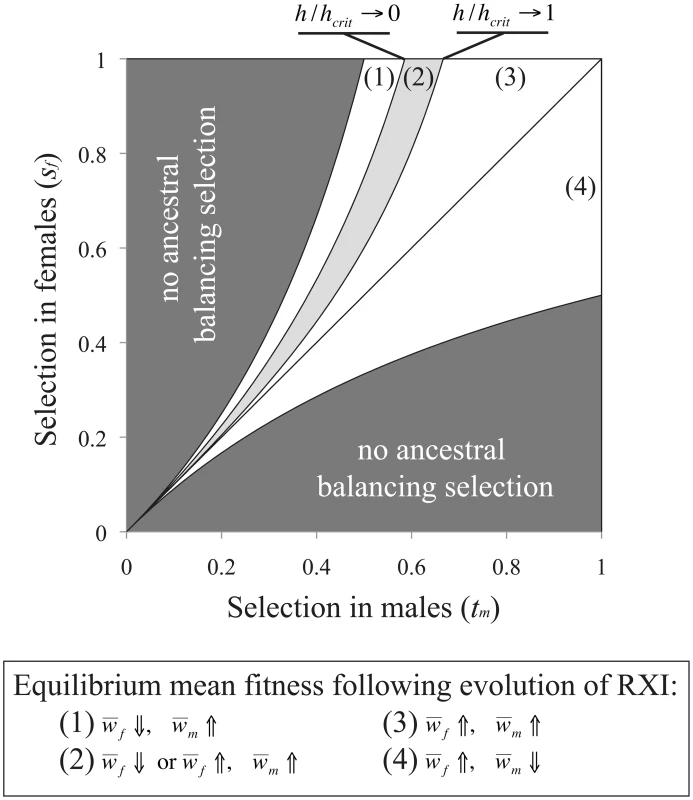
In an ancestral population with PXI, and segregating for a sexually antagonistic balanced polymorphism, unbiased RXI is favored and may evolve when h<hcrit = (1−tm)/(2−tm). Following such an evolutionary transition, the male-beneficial/female-detrimental allele approaches a new equilibrium frequency, and mean fitness per sex evolves to a new equilibrium. For the model of sexually antagonistic genetic variation, our analysis of the change in equilibrium mean fitness follows the evolution of the ancestrally polymorphic locus, and ignores any sexually antagonistic X-linked mutations that might enter the population following the transition to RXI. However, the parameter space that permits an X-linked sexually antagonistic polymorphism is larger under RXI than PXI, within the relevant parameter space where RXI can evolve (PXI can nevertheless be more conducive to polymorphism under alternative dominance parameterizations [52]), and recessive sexually antagonistic alleles that benefit males weakly can more readily be maintained [54], [71]. Therefore, the evolution of RXI could increase the parameter space that permits X-linked sexually antagonistic polymorphism. Antagonistically selected X-linked loci that could not establish balanced polymorphisms in the ancestral population with PXI may do so in an RXI population. In the longer-term, this could increase male and decrease female fitness, contingent on the specific distribution of male and female selection and dominance coefficients among sexually antagonistic mutations.
The evolution of biased RXI
Thus far we have shown that RXI can be favored by selection if female-detrimental alleles are sufficiently masked when heterozygous. However, selection might not necessarily favor the same rate of inactivation for maternally and paternally derived X chromosomes in females. Sex-differential selection generates allele frequency differences between males and females, which can favor differential expression of genes inherited from opposite-sex parents [40]. With respect to the mammalian X, polymorphism under sex-differential selection might favor the evolution of unequal inactivation rates between paternally and maternally derived X chromosomes; this is conceptually similar to genomic imprinting that involves partial, but unequal, expression of both of the parental gene copies [72]–[79]. Because X inactivation is a female-limited trait, we expect that selection will favor preferential inactivation of the chromosome with a greater probability of carrying female-deleterious alleles.
We tested this intuition by performing an invasion analysis ([46], chapter 12) to determine the evolutionary stability of different X inactivation strategies. To characterize the direction and magnitude of the bias favored by selection, we consider a population initially fixed for an arbitrary inactivation strategy, ξ11 (0<ξ11<1), and at equilibrium for fitness variation given this strategy [e.g., eqs. (1–2)], and identify the ξ11 values that are stable to invasion by an allele that alters the X inactivation ratio of female carriers (i.e. the “evolutionarily stable strategies” [80]).
Under a mutation-selection balance model, the stable paternal X inactivation value () is:
The exponent term [−ln(2)/ln(2h)] is positive when A1 is at least partially recessive (h<½), which we assume here and below, and the ratio determines the direction of bias favored by selection. Selection favors preferential inactivation of the paternal X when deleterious alleles are more frequently transmitted to progeny through males than females (>½ when <1), and favors preferential inactivation of the maternal X when deleterious mutations are more frequently transmitted through females (<½ when >1). Eq. (7) can be expressed as an explicit function of the selection and dominance coefficients by assuming that sfh≪1 (this is biologically reasonable given the observed negative association between dominance and effect size of deleterious mutations [12]). The critical ratio becomes: Selection favors preferential inactivation of the maternally derived X when sm>sfh, and the degree of bias may be pronounced when deleterious mutations are poorly masked in females (e.g., when h is closer to ½ than to zero; Figure 4).Fig. 4. Sex-differential selection favors the evolution of biased RXI. 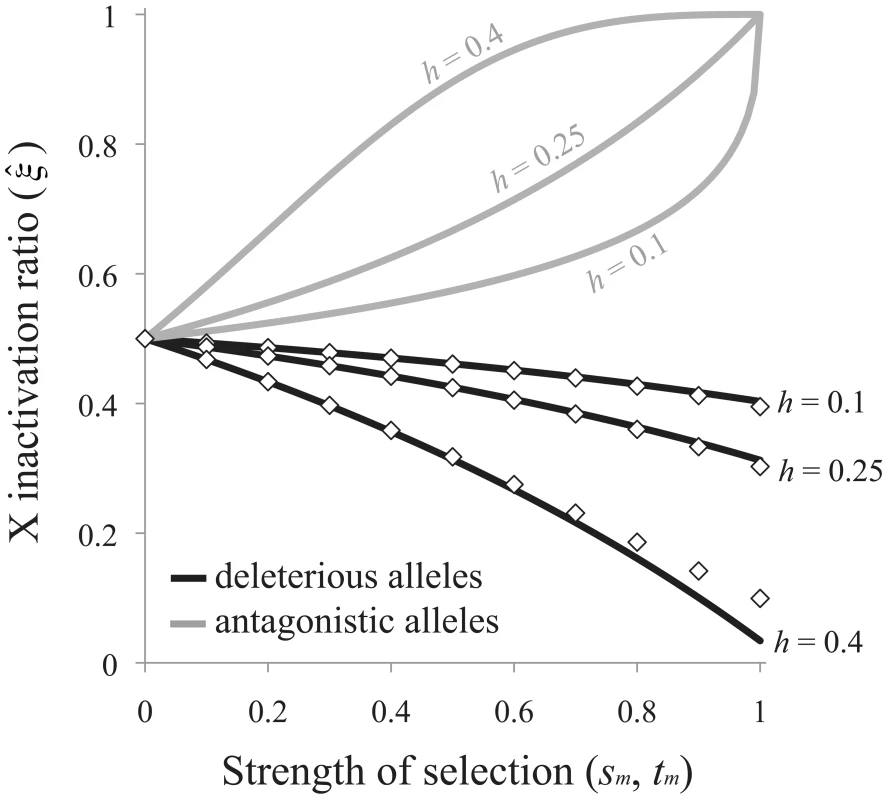
Black curves are based on eq. (8) for the mutation-selection balance model of genetic variation; diamonds are based on numerical evaluation of the more exact eq. (7). Gray curves are based on eq. (9) for sexually antagonistic alleles maintained by balancing selection. Results for the mutation-selection balance case assume equal male and female selection coefficients (sm = sf). Biases are further accentuated when sm>sf; biases may be dampened or reversed when sm<sf. Adopting the same analytical approach for the case of sexually antagonistic fitness variation, the equilibrium X inactivation rule is:
Given the stated parameter constraints (h<½; 1>tm>0), (1−tm)−ln(2)/ln(2h) will always be positive and less than one, and selection always favors preferential inactivation of the paternally inherited X chromosome. The magnitude of this bias increases with tm and h, similar to the deleterious mutation scenario for fitness variation (Figure 4). When either the selection or the dominance coefficient is sufficiently large, both models of fitness variation can favor large X inactivation biases. Some moderate values of s, t and h (to the left of the x-axis in Figure 4) could lead to large enough biases – on the order of a few percent or more – to be empirically detectable.Discussion
X inactivation in mammals can take a variety of specific forms, ranging from strict PXI, to various forms of RXI [1], [2], [6], [7]. This range of observed diversity is particularly striking, as quantitative analyses of the maternally to paternally derived X inactivation ratio are available for relatively few mammalian species to date (the best data coming from a subset of mouse and human tissues). Modern high-throughput, genome-wide and allele-specific gene expression technologies (such as RNA-seq), can now be used to systematically analyze X inactivation ratios in any number of mammalian species or tissues [6], [81], and this new technology promises to reveal much more diversity in X inactivation patterns.
The range of X inactivation rules employed by different species might usefully be considered within a theoretical framework of sex-differential selection. The population genetic models analyzed here reveal broad opportunities for X inactivation evolution, though it is important to note that model predictions hinge upon the capacity of X inactivation ratios to evolve (i.e., there must be genetic variation for X inactivation rules). There is some evidence for alleles in mice that affect X inactivation choice (reviewed in [82], [83]). Moreover, the observed range of X inactivation patterns between mice, humans, and marsupials (see introduction) imply at least some degree of evolutionary lability for the trait. On the other hand, maternally biased X inactivation has not been observed, and it is unclear whether this reflects under-sampling (the phenomenon may exist, but has yet to be documented), intrinsic genetic constraints (as mentioned), or that biased inactivation of the maternally derived X is generally unfavorable. The evolvability of the X inactivation ratio should be considered an important issue that warrants future study.
Multiple genes, conflicting patterns of selection, and the evolution of genomic imprinting
For reasons of tractability, and in parallel with theory on the evolution of diploidy (e.g., [26], [45]; chapter 8 of [46]), we have focused our analysis on two-locus population genetics models to characterize how different forms of fitness variation and linkage will influence patterns of selection for different X inactivation rules. However, X inactivation affects the expression of many genes simultaneously, and unique patterns of genetic variation among X-linked loci could individually favor discordant X inactivation strategies. We can gain some insight into scenarios that involve multiple X-linked loci, under the assumption that each polymorphic locus contributes independently to selection on a rare, unlinked modifier allele (i.e., we assume loose linkage and no epistasis between fitness loci; net fitness effects of multi-gene haplotypes could instead apply under tight linkage between fitness loci). Under these conditions, criteria for invasion of a modifier allele will be , where λi is the leading eigenvalue associated with the two-locus system for the modifier locus and the ith of n X-linked fitness loci (i = {1, 2, …, n}) [84], [85]. With weak effects of individual fitness loci on the modifier (i.e., λi≈1), the selection coefficient associated with a rare modifier allele will be smod≈nE(λi−1), where E(λi−1) represents the arithmetic mean, and λi−1 represents selection contributed by the ith locus (invasion of the modifier allele requires that smod>0).
To the extent that X-linked loci segregate for deleterious alleles, and these have similar selection and dominance coefficients, the net effects of multiple X-linked loci on a modifier will be reinforcing, and the strength of selection on the X inactivation strategy will increase with the number of contributing loci (i.e., if E(λi−1)≠0, then smod scales approximately linearly with n, the number of contributing loci; this scaling is in agreement with multilocus models for the evolution of diploidy [28]). Although little available data directly bear upon the sex-specific selection and dominance parameters of mammalian X-linked mutations, data from other systems suggest that most mutations have small, at least partially recessive fitness effects (e.g., [12]–[15], [86]), and are deleterious to both sexes [35], [36]. If X-linked mutations have similarly small selection and dominance coefficients under RXI, then fitness variation due to deleterious alleles might favor the evolution of relatively unbiased RXI rules.
Genes that are polymorphic for sexually antagonistic alleles could exert disproportionately strong influence on the evolutionary trajectories of X inactivation evolution. Sexually antagonistic alleles generate selection of a higher order of magnitude than loci at mutation-selection balance (Figure S1). Consequently, selection due to sexually antagonistic polymorphism may plausibly eclipse the cumulative effects of selection from deleterious alleles. The relative contribution of deleterious versus antagonistically selected alleles to X-linked fitness variation is ultimately an empirical question. To the extent that sexually antagonistic fitness variation is common in mammalian populations (as may indeed be the case; e.g., [60], [64]), selection should favor the evolution of biased inactivation of the paternally inherited X.
Conflicts between different X-linked loci over the optimal ratio of maternal to paternal X inactivation could potentially be resolved by the evolution of genomic imprinting at individual X-linked genes. Previous models have considered two scenarios of sexually antagonistic selection driving the evolution of imprinting (i.e., the partial or complete silencing of a maternally or a paternally inherited copy of a single gene; [72]–[79]). First, when the optimal transcription level of a X-linked gene differs between males and females, imprinting can facilitate sex-specific adaptation by generating sexually dimorphic gene expression [41], [42]. Imprinting of the maternally inherited gene is favored under selection for higher transcription levels in females, whereas paternal imprinting is favored at genes selected for higher transcription in males [41]–[43]. Second, in genes polymorphic for sexually antagonistic alleles, sexually dimorphic imprinting can mitigate fitness costs of inheriting harmful alleles, which are preferentially transmitted from opposite-sex parents [40]. Existing models of this latter scenario consider polymorphism and imprinting at an autosomal gene [40], [44], yet the basic processes should apply to the X (as discussed in [40]) – particularly so because X-linkage promotes allele frequency differences and asymmetrical imprinting effects between males and females [41], [42], [87]. X inactivation and gene-by-gene imprinting may serve as complementary mechanisms for optimizing male and female fitness.
Evolutionary transitions between RXI and PXI
Evolution of RXI from an ancestral population with PXI should be relatively unconstrained, provided three conditions are met: (i) there is genetic variation for RXI (i.e., it is evolvable; see above); (ii) X-linked fitness variation is largely caused by segregating deleterious mutations; and (iii) the fitness costs of these mutations are at least partially masked under RXI (i.e., h<½, as seems likely). The availability of mutations to RXI could potentially constrain the convergent evolution of RXI in marsupials [18]. Sexually antagonistic X-linked fitness variability, if common within marsupials, could also promote the evolutionary maintenance of PXI. This hypothesis is plausible, given the pronounced sexual size dimorphism in marsupials relative to other mammalian species (e.g., [88], [89]). Such dimorphism is indicative of strong sexual selection, which could promote the accumulation of sexually antagonistic genetic variation and thereby limit opportunities to evolve RXI.
Once RXI has evolved, evolutionary reversals to strict PXI should face severe evolutionary constraints. In populations with RXI, the filtering of genetic variation by selection in females will strongly depend upon dominance. RXI permits the preferential accumulation of recessive, female-deleterious mutations, because such alleles experience weakened purifying selection. The retention of recessive alleles in populations with RXI should downwardly shift the mean dominance of segregating alleles (relative to the dominance coefficients of spontaneous mutations; e.g., [12], [90]), and increase the cost to females of becoming homozygous or effectively haploid, as they would under PXI. Filtering of mutations based on their dominance coefficients does not eliminate opportunities to evolve biased RXI, but it should severely constrain evolutionary transitions to complete PXI, which completely eliminates effects of masking. This situation is analogous to the coevolution of outcrossing rates and inbreeding depression, with the latter expected to become more severe in outbreeding populations because they shelter recessive alleles from natural selection [91], [92].
Species diversity for X inactivation strategies
Species-specific properties of mutation and genetic variation might predictably affect patterns of selection for different X inactivation strategies. Sexual selection and sex-biased mutation rates are each likely to vary among species, and both processes can influence the relative transmission probabilities of female-deleterious alleles between maternally and paternally derived X chromosomes.
Mammalian mutation rates are often higher in males than females [93], [94], which tends to upwardly bias paternal transmission of deleterious alleles. Consider a population with unbiased RXI and a mutation rate of um and uf in males and females, respectively (see Text S1). With unbiased mutation (um = uf), selection can favor reduced expression of the maternally inherited X when sfh<sm, as implied by eq. (8). Male-biased mutation (um/uf>1) reduces this parameter space to (um/uf)sfh<sm, because males transmit a higher fraction of de-novo mutations to their daughters. We predict that preferential inactivation of the paternally inherited X will be more common (or more severe) in species with strongly male-biased mutation rates.
Sexual selection could similarly favor paternally biased X inactivation. Although strong purifying selection in males via sexual selection can reduce paternal transmission rates of deleterious alleles ([33], [35], [36]; though not all data support this possibility, e.g.: [95], [96]), it will also reduce the frequencies and contributions of deleterious alleles to fitness variation in females. Sexual selection may simultaneously increase the pervasiveness of sexual antagonism [97] and the contribution of sexually antagonistic alleles to female fitness variation. If sexually antagonistic fitness variation increases with the strength of sexual selection, then so should the degree of paternally biased X inactivation.
Methods
X-linked modifier model
Haplotype frequency recursions
In a given generation, let the haplotype frequencies in eggs be x1 = [A1B1], x2 = [A2B1], x3 = [A1B2], and x4 = [A2B2]. Haplotype frequencies in sperm are y1 = [A1B1], y2 = [A2B1], y3 = [A1B2], and y4 = [A2B2]. Following random mating, females of the next generation will carry a maternally inherited haplotype i = {1, 2, 3, 4} and paternally inherited haplotype j = {1, 2, 3, 4} with probability xiyj. Males of the next generation inherit a single haplotype i from their mothers, with probability xi. The fitness of a female carrying haplotypes i and j is fij, and the fitness of males carrying haplotype i is mi. Haplotype frequencies after selection and recombination, but prior to mutation, are described by the following set of recursion equations:
where F is the sum of the numerators of x1′, x2′, x3′, and x4′; M is the sum of numerators of y1′, y2′, y3′, and y4′; and Θ = x1y4f14−x2y3f23−x3y2f32+x4y1f41.For the mutation-selection balance scenario, we consider fitness variation contributed by alleles that are deleterious to both sexes, and arbitrarily assume that A1 is the deleterious allele. Assuming mutation rates at locus A are much smaller than the strength of selection against A1, mutations from A1 to A2 can be safely ignored. The frequency of each haplotype after a single generation, including mutation, will be:
where u is the mutation rate at the A locus, per gamete. When variation is maintained by sexual antagonism (that is, a balanced polymorphism is stably maintained), recurrent mutation will marginally affect equilibrium allele frequencies at the A locus [55]. Therefore, the recursion equations from eq. (10) are sufficient to describe haplotype frequency dynamics under sexual antagonism.Invasion conditions for B2 alleles
Jacobian matrices were calculated for the two models of genetic variation for fitness (see Text S2), with each model giving rise to a block triangular matrix with two diagonal submatrices (see [46], chapter 12). In each model, invasion of the B2 allele is favored when the leading eigenvalue of the Jacobian is greater than one; B2 cannot invade when the leading eigenvalue is less than one. One submatrix has leading eigenvalue less than one as a condition of the population initially being fixed for B1 and at stable equilibrium at the A locus. Stability at B is therefore determined by the leading eigenvalue of the remaining submatrix, J (see Table S1 and Text S2).
Under the mutation-selection balance model for fitness variation, the characteristic polynomial is:
where the partial derivatives are evaluated from the recursions in eq. (11), each evaluated at the equilibrium: = x1 = 1−x2, = y1 = 1−y2, and x3 = x4 = y3 = y4 = 0, with values of and based on eq. (1). The leading eigenvalue is the largest of the roots of λ. Under the sexual antagonism model, the characteristic polynomial is: where partial derivatives are calculated from recursions in eq. (10), each evaluated at the equilibrium: = x1 = 1−x2, = y1 = 1−y2, and x3 = x4 = y3 = y4 = 0, with values of and based on eq. (2).Stability criteria (i.e., whether the leading eigenvalue was greater or less than zero) were determined by hand, and leading eigenvalues were obtained numerically by Newton-Raphson iteration.
Autosomal modifier model
When the modifier locus, B, is linked to an autosome, the haplotype recursions can again be obtained using similar approaches as described above. Here, the frequency of each haplotype in females will be the same as described above for the specific case of free recombination: r = ½. Haplotype frequencies in males, following selection and meiosis, are modified to:
where m1 = m3, m2 = m4, and M = (x1+x3)m1+(x2+x4)m2.Stability analysis (invasion opportunities for rare B2 alleles) follows the same approach as before, with initial conditions of variation at locus A remaining unchanged. Under the case of variation maintained by sexually antagonistic selection, effects of mutation are ignored (we set u to zero). The generic characteristic polynomial is:
with the partial derivatives each evaluated at the equilibrium: = x1 = 1−x2, = y1 = 1−y2, and x3 = x4 = y3 = y4 = 0. Values of and are based on eqs. (1) or (2) as appropriate.Supporting Information
Zdroje
1. PayerB, LeeJT (2008) X chromosome dosage compensation: how mammals keep the balance. Ann Rev Genet 42 : 733–772.
2. DeakinJE, ChaumeilJ, HoreTA, GravesJAM (2009) Unravelling the evolutionary origins of X chromosome inactivation in mammals: insights from marsupials and monotremes. Chromosome Research 17 : 671–685.
3. CooperDW, VandeBergJL, SharmanGB, PooleWE (1971) Phosphoglycerate kinase polymorphism in kangaroos provides further evidence for paternal X inactivation. Nature New Biology 230 : 155–157.
4. SharmanGB (1971) Late DNA replication in the paternally derived X chromosome of female kangaroos. Nature 230 : 231–232.
5. LyonMF (1961) Gene action in the X-chromosome of the mouse (Mus musculus L.). Nature 190 : 372–373.
6. WangX, SolowayPD, ClarkAG (2010) Paternally biased X inactivation in mouse neonatal brain. Genome Biology 11: R79.
7. GreggC, ZhangJ, ButlerJE, HaigD, DulacC (2010) Sex-specific parent-of-origin allelic expression in the mouse brain. Science 329 : 682–685.
8. CooperDW, JohnstonPG, GravesJAM (1993) X-inactivation in marsupials and monotremes. Seminars in Developmental Biology 4 : 117–128.
9. ChandraHS, BrownSW (1975) Chromosome imprinting and the mammalian X chromosome. Nature 253 : 165–168.
10. CharlesworthB (1978) Model for evolution of Y chromosomes and dosage compensation. Proc Natl Acad Sci USA 75 : 5618–5622.
11. CharlesworthB (1996) The evolution of chromosomal sex determination and dosage compensation. Current Biology 6 : 149–162.
12. SimmonsMJ, CrowJF (1977) Mutations affecting fitness in Drosophila populations. Ann Rev Genet 11 : 49–78.
13. CharlesworthB, CharlesworthD (1999) The genetic basis of inbreeding depression. Genet Res 74 : 329–340.
14. Charlesworth B, Hughes KA (1999) The maintenance of genetic variation in life-history traits. Pp. 369–392 in RS Singh and CB Krimbas, eds. Evolutionary genetics: from molecules to morphology, vol. 1 Cambridge University Press, Cambridge, UK.
15. HalliganDL, KeightleyPD (2009) Spontaneous mutation accumulation studies in evolutionary genetics. Annu Rev Ecol Evol Syst 40 : 151–172.
16. LyonMF (1988) The William Allan Memorial Award Address: X-chromosome inactivation and the location and expression of X-linked genes. Am J Hum Genet 42 : 8–16.
17. MooreT, HaigD (1991) Genomic imprinting in mammalian development: a parental tug-of-war. Trends in Genetics 7 : 45–49.
18. HaigD (2006) Self-imposed silence: parental antagonism and the evolution of X-chromosome inactivation. Evolution 60 : 440–447.
19. EngelstädterJ, HaigD (2008) Sexual antagonism and the evolution of X chromosome inactivation. Evolution 62 : 2097–2104.
20. MankJE (2009) The W, X, Y and Z of sex-chromosome dosage compensation. Trends Genet 25 : 226–233.
21. CrowJF, KimuraM (1965) Evolution in sexual and asexual populations. Am Nat 99 : 439–450.
22. CharlesworthB (1991) When to be diploid. Nature 351 : 273–274.
23. KondrashovAS, CrowJF (1991) Haploidy or diploidy: which is better? Nature 351 : 314–315.
24. PerrotV, RicherdS, ValéroM (1991) Transition from haploidy to diploidy. Nature 351 : 315–317.
25. OttoSP, GersteinAC (2008) The evolution of haploidy and diploidy. Current Biology 18: R1121–R1124.
26. OttoSP, GoldsteinDB (1992) Recombination and the evolution of diploidy. Genetics 131 : 745–751.
27. BengtssonBO (1992) Deleterious mutations and the origin of the meiotic ploidy cycle. Genetics 131 : 741–744.
28. JenkinsCD, KirkpatrickM (1995) Deleterious mutation and the evolution of genetic life cycles. Evolution 49 : 512–520.
29. OttoSP, MarksJC (1996) Mating systems and the evolutionary transition between haploid and diploidy. Biol J Linnean Soc 57 : 197–218.
30. HallDW (2000) The evolution of haploid, diploid and polymorphic haploid-diploid life cycles: the role of meiotic mutation. Genetics 156 : 893–898.
31. OrrHA (1995) Somatic mutation favors the evolution of diploidy. Genetics 139 : 1441–1447.
32. VicosoB, CharlesworthB (2006) Evolution on the X chromosome: unusual patterns and processes. Nat Rev Genet 7 : 645–653.
33. WhitlockMC, AgrawalAF (2009) Purging the genome with sexual selection: reducing mutation load through selection on males. Evolution 63 : 569–582.
34. ConnallonT, CoxRM, CalsbeekR (2010) Fitness consequences of sex-specific selection. Evolution 64 : 1671–1682.
35. MalletMA, BouchardJM, KimberCM, ChippindaleAK (2011) Experimental mutation-accumulation on the X chromosome of Drosophila melanogaster reveals stronger selection on males than females. BMC Evol Biol 11 : 156.
36. SharpNP, AgrawalAF (2012) Male-biased fitness effects of spontaneous mutations in Drosophila melanogaster. Evolution DOI:10.1111/j.1558-5646.2012.01834.x.
37. BondurianskyR, ChenowethSF (2009) Intralocus sexual conflict. Trends Ecol Evol 24 : 280–288.
38. van DoornGS (2009) Intralocus sexual conflict. Ann NY Acad Sci 1168 : 52–71.
39. KidwellJF, CleggMT, StewartFM, ProutT (1977) Regions of stable equilibria for models of differential selection in the two sexes. Genetics 85 : 171–183.
40. DayT, BondurianskyR (2004) Intralocus sexual conflict can drive the evolution of genomic imprinting. Genetics 167 : 1537–1546.
41. IwasaY, PomiankowskiA (1999) Sex specific X chromosome expression caused by genomic imprinting. J Theor Biol 197 : 487–495.
42. IwasaY, PomiankowskiA (2001) The evolution of X-linked genomic imprinting. Genetics 158 : 1801–1809.
43. SeymourRM, PomiankowskiA (2006) ESS gene expression of X-linked imprinted genes subject to sexual selection. J Theor Biol 241 : 81–93.
44. Van CleveJ, FeldmanMW (2007) Sex-specific viability, sex linkage and dominance in genomic imprinting. Genetics 176 : 1101–1118.
45. MableBK, OttoSP (1998) The evolution of life cycles with haploid and diploid phases. Bio Essays 20 : 453–462.
46. Otto SP, Day T (2007) A biologist's guide to mathematical modeling in ecology and evolution. Princeton University press, Princeton, NJ.
47. DobynsWB, FilauroA, TomsonBN, ChanAS, AllenWH, TingNT, OosterwijkJC, OberC (2004) Inheritance of most X-linked traits is not dominant or recessive, just X-linked. Am J Med Genet 129A: 136–143.
48. RavignéV, DieckmannU, OlivieriI (2009) Live where you thrive: joint evolution of habitat choice and local adaptation facilitates specialization and promotes diversity. Am Nat 174: E141–E169.
49. ConnallonT, ClarkAG (2011) The resolution of sexual antagonism by gene duplication. Genetics 187 : 919–937.
50. GuillaumeF, OttoSP (2012) Gene functional trade-offs and the evolution of pleiotropy. Genetics 192 : 1389–1409.
51. MankJE, VicosoB, BerlinS, CharlesworthB (2010) Effective population size and the faster-X effect: Empiricial results and their interpretation. Evolution 64 : 663–674.
52. SantureAW, SpencerH (2012) Genomic imprinting leads to less selectively maintained polymorphism on X chromosomes. Genetics 192 : 1455–1464.
53. CooperDW (1976) Studies on metatherian sex chromosomes II: the improbability of a stable balanced polymorphism at an X-linked locus with the paternal X inactivation system of kangaroos. Aust J Biol Sci 29 : 245–250.
54. PattenMM, HaigD (2009) Maintenance or loss of genetic variation under sexual and parental antagonism at a sex-linked locus. Evolution 63 : 2888–2895.
55. ConnallonT, ClarkAG (2012) A general population genetic framework for antagonistic selection that accounts for demography and recurrent mutation. Genetics 190 : 1477–1489.
56. MullonC, PomiankowskiA, ReuterM (2012) The effects of selection and genetic drift on the genomic distribution of sexually antagonistic alleles. Evolution 66 : 3743–3753.
57. MankJE, HoskenDJ, WedellN (2011) Some inconvenient truths about sex chromosome dosage compensation and the potential role of sexual conflict. Evolution 65 : 2133–2144.
58. ChippindaleAK, GibsonJR, RiceWR (2001) Negative genetic correlation for adult fitness between sexes reveals ontogenetic conflict in Drosophila. Proc Natl Acad Sci USA 98 : 1671–1675.
59. FedorkaKM, MousseauTA (2004) Female mating bias results in conflicting sex-specific offspring fitness. Nature 429 : 65–67.
60. FoersterK, CoulsonT, SheldonBC, PembertonJM, Clutton-BrockTH, KruukLEB (2007) Sexually antagonistic genetic variation for fitness in red deer. Nature 447 : 1107–1110.
61. BrommerJE, KirkpatrickM, QvarnströmA, GustafssonL (2007) The intersexual genetic correlation for lifetime fitness in the wild and its implications for sexual selection. PLoS ONE 2: e744 doi:10.1371/journal.pone.0000744.
62. CoxRM, CalsbeekR (2010) Cryptic sex-ratio bias provides indirect genetic benefits despite sexual conflict. Science 328 : 92–94.
63. InnocentiP, MorrowEH (2010) The sexually antagonistic genes of Drosophila melanogaster. PLoS Biol 8: e1000335 doi:10.1371/journal.pbio.1000335.
64. MokkonenM, KokkoH, KoskelaE, LehtonenJ, MappesT, MartiskainenH, MillsSC (2011) Negative frequency-dependent selection of sexually antagonistic alleles in Myodes glareolus. Science 334 : 972–974.
65. DelphLF, AndicoecheaJ, StevenJC, HerlihyCR, ScarpinoSV, BellDL (2011) Environment-dependent intralocus sexual conflict in a dioecious plant. New Phytologist 192 : 542–552.
66. LewisZ, WedellN, HuntJ (2011) Evidence for strong intralocus sexual conflict in the Indian meal moth. Evolution 65 : 2085–2097.
67. HaldaneJBS (1937) The effect of variation on fitness. Am Nat 71 : 337–349.
68. SpencerHG, WilliamsMJM (1997) The evolution of genomic imprinting: two modifier-locus models. Theor Pop Biol 51 : 23–35.
69. OttoSP, YongP (2002) The evolution of gene duplicates. Homol Eff 46 : 451–483.
70. ConnallonT, ClarkAG (2010) Gene duplication, gene conversion and the evolution of the Y chromosome. Genetics 186 : 277–286.
71. RiceWR (1984) Sex chromosomes and the evolution of sexual dimorphism. Evolution 38 : 735–742.
72. BarlowDP (2011) Genomic imprinting: a mammalian epigenetic discovery model. Annu Rev Genet 45 : 379–403.
73. SpencerHG, FeldmanMW, ClarkAG (1998) Genetic conflicts, multiple paternity and the evolution of genomic imprinting. Genetics 148 : 893–904.
74. SpencerHG, ClarkAG, FeldmanMW (1999) Genetic conflicts and the evolutionary origin of genomic imprinting. Trends Ecol Evol 14 : 197–201.
75. HaigD (2000) The kinship theory of genomic imprinting. Annu Rev Ecol Syst 31 : 9–32.
76. WilkinsJF, HaigD (2003) What good is genomic imprinting: the function of parent specific gene expression. Nat Rev Genet 4 : 359–368.
77. SpencerHG, FeldmanMW, ClarkAG, WeissteinAE (2004) The effect of genetic conflict on genomic imprinting and modification of expression at a sex-linked locus. Genetics 166 : 565–579.
78. BrandvainY (2010) Matrisibs, patrisibs, and the evolution of imprinting on autosomes and sex chromosomes. Am Nat 176 : 511–521.
79. BrandvainY, Van CleveJ, UbedaF, WilkinsJF (2011) Demography, kinship, and the evolving theory of genomic imprinting. Trends Genet 27 : 251–257.
80. Maynard SmithM, PriceGR (1973) The logic of animal conflict. Nature 246 : 15–18.
81. RozowskyJ, AbyzovA, WangJ, AlvesP, RahaD, HarmanciA, LengJ, BjornsonR, KongY, KitabayashiN, BhardwajN, RubinM, SnyderM, GersteinM (2011) AlleleSeq: analysis of allele-specific expression and binding in a network framework. Mol Syst Biol 7 : 522.
82. ClercP, AvnerP (2006) Random X-chromosome inactivation: skewing lessons for mice and men. Curr Op Genet Dev 16 : 246–253.
83. ThorvaldsenJL, KrappC, HuntingtonFW, BartolomeiMS (2012) Nonrandom X chromosome inactivation is influenced by multiple regions of the murine X chromosome. Genetics 192 : 1095–1107.
84. OttoSP, BourguetD (1999) Balanced polymorphisms and the evolution of dominance. Am Nat 153 : 561–574.
85. HoughJ, ImmlerS, BarrettSCH, OttoSP (2013) Evolutionary stable sex ratios and mutation load. Evolution in press.
86. AgrawalAF, WhitlockMC (2011) Inferences about the distribution of dominance drawn from yeast gene knockout data? Genetics 178 : 553–566.
87. Crow JF, Kimura M (1970) An introduction to population genetics theory. Harper and Row, New York.
88. WeckerlyFW (1998) Sexual-size dimorphism: influence of mass and mating systems in the most dimorphic mammals. J Mammology 79 : 33–52.
89. Lindenfors P, Gittleman JL, Jones KE (2007) Sexual size dimorphism in mammals. In Fairbairn DJ, Blanckenhorn WU, Székely T, eds. Sex, Size and Gender Roles, pp. 16–26. Oxford University Press, Oxford.
90. MukaiT (1969) The genetic structure of natural populations of Drosophila melanogaster. VIII. Natural selection on the degree of dominance of viability polygenes. Genetics 63 : 467–478.
91. LandeR, SchemskeDW (1985) The evolution of self-fertilization and inbreeding depression in plants. I. Genetic models. Evolution 39 : 24–40.
92. CharlesworthB, CharlesworthD (1998) Some evolutionary consequences of deleterious mutations. Genetica 102/103 : 3–19.
93. EllegrenH (2007) Characteristics, causes and evolutionary consequences of male-biased mutation. Proc Roy Soc B 274 : 1–10.
94. SayresMA, MakovaKD (2011) Genome analyses substantiate male mutation bias in many species. Bioessays 33 : 938–945.
95. HollisB, HouleD (2011) Populations with elevated mutation load do not benefit from the operation of sexual selection. J Evol Biol 24 : 1918–1926.
96. ArbuthnottD, RundleHD (2012) Sexual selection is ineffectual or inhibits the purging of deleterious mutations in Drosophila melanogaster. Evolution 66 : 2127–2137.
97. CoxRM, CalsbeekR (2009) Sexually antagonistic selection, sexual dimorphism, and the resolution of intralocus sexual conflict. Am Nat 173 : 176–187.
Štítky
Genetika Reprodukční medicína
Článek The G4 GenomeČlánek Mondo/ChREBP-Mlx-Regulated Transcriptional Network Is Essential for Dietary Sugar Tolerance inČlánek RpoS Plays a Central Role in the SOS Induction by Sub-Lethal Aminoglycoside Concentrations inČlánek Tissue Homeostasis in the Wing Disc of : Immediate Response to Massive Damage during DevelopmentČlánek Disruption of TTDA Results in Complete Nucleotide Excision Repair Deficiency and Embryonic LethalityČlánek DJ-1 Decreases Neural Sensitivity to Stress by Negatively Regulating Daxx-Like Protein through dFOXO
Článek vyšel v časopisePLOS Genetics
Nejčtenější tento týden
2013 Číslo 4
-
Všechny články tohoto čísla
- Epigenetic Upregulation of lncRNAs at 13q14.3 in Leukemia Is Linked to the Downregulation of a Gene Cluster That Targets NF-kB
- A Big Catch for Germ Cell Tumour Research
- The Quest for the Identification of Genetic Variants in Unexplained Cardiac Arrest and Idiopathic Ventricular Fibrillation
- A Nonsynonymous Polymorphism in as a Risk Factor for Human Unexplained Cardiac Arrest with Documented Ventricular Fibrillation
- The Hourglass and the Early Conservation Models—Co-Existing Patterns of Developmental Constraints in Vertebrates
- Smaug/SAMD4A Restores Translational Activity of CUGBP1 and Suppresses CUG-Induced Myopathy
- Balancing Selection on a Regulatory Region Exhibiting Ancient Variation That Predates Human–Neandertal Divergence
- The G4 Genome
- Extensive Natural Epigenetic Variation at a Originated Gene
- Mouse Oocyte Methylomes at Base Resolution Reveal Genome-Wide Accumulation of Non-CpG Methylation and Role of DNA Methyltransferases
- The Environment Affects Epistatic Interactions to Alter the Topology of an Empirical Fitness Landscape
- TIP48/Reptin and H2A.Z Requirement for Initiating Chromatin Remodeling in Estrogen-Activated Transcription
- Aconitase Causes Iron Toxicity in Mutants
- Tbx2 Terminates Shh/Fgf Signaling in the Developing Mouse Limb Bud by Direct Repression of
- Mondo/ChREBP-Mlx-Regulated Transcriptional Network Is Essential for Dietary Sugar Tolerance in
- Sex-Differential Selection and the Evolution of X Inactivation Strategies
- Identification of a Tissue-Selective Heat Shock Response Regulatory Network
- Phosphorylation-Coupled Proteolysis of the Transcription Factor MYC2 Is Important for Jasmonate-Signaled Plant Immunity
- RpoS Plays a Central Role in the SOS Induction by Sub-Lethal Aminoglycoside Concentrations in
- Six Homeoproteins Directly Activate Expression in the Gene Regulatory Networks That Control Early Myogenesis
- Rtt109 Prevents Hyper-Amplification of Ribosomal RNA Genes through Histone Modification in Budding Yeast
- ATP-Dependent Chromatin Remodeling by Cockayne Syndrome Protein B and NAP1-Like Histone Chaperones Is Required for Efficient Transcription-Coupled DNA Repair
- Iron-Responsive miR-485-3p Regulates Cellular Iron Homeostasis by Targeting Ferroportin
- Mutations in Predispose Zebrafish and Humans to Seminomas
- Cytotoxic Chromosomal Targeting by CRISPR/Cas Systems Can Reshape Bacterial Genomes and Expel or Remodel Pathogenicity Islands
- Tissue Homeostasis in the Wing Disc of : Immediate Response to Massive Damage during Development
- All SNPs Are Not Created Equal: Genome-Wide Association Studies Reveal a Consistent Pattern of Enrichment among Functionally Annotated SNPs
- Functional 358Ala Allele Impairs Classical IL-6 Receptor Signaling and Influences Risk of Diverse Inflammatory Diseases
- The Tissue-Specific RNA Binding Protein T-STAR Controls Regional Splicing Patterns of Pre-mRNAs in the Brain
- Neutral Genomic Microevolution of a Recently Emerged Pathogen, Serovar Agona
- Genetic Requirements for Signaling from an Autoactive Plant NB-LRR Intracellular Innate Immune Receptor
- SNF5 Is an Essential Executor of Epigenetic Regulation during Differentiation
- Dialects of the DNA Uptake Sequence in
- Reference-Free Population Genomics from Next-Generation Transcriptome Data and the Vertebrate–Invertebrate Gap
- Senataxin Plays an Essential Role with DNA Damage Response Proteins in Meiotic Recombination and Gene Silencing
- High-Resolution Mapping of Spontaneous Mitotic Recombination Hotspots on the 1.1 Mb Arm of Yeast Chromosome IV
- Rod Monochromacy and the Coevolution of Cetacean Retinal Opsins
- Evolution after Introduction of a Novel Metabolic Pathway Consistently Leads to Restoration of Wild-Type Physiology
- Disruption of TTDA Results in Complete Nucleotide Excision Repair Deficiency and Embryonic Lethality
- Insulators Target Active Genes to Transcription Factories and Polycomb-Repressed Genes to Polycomb Bodies
- Signatures of Diversifying Selection in European Pig Breeds
- The Chromosomal Passenger Protein Birc5b Organizes Microfilaments and Germ Plasm in the Zebrafish Embryo
- The Histone Demethylase Jarid1b Ensures Faithful Mouse Development by Protecting Developmental Genes from Aberrant H3K4me3
- Regulates Synaptic Development and Endocytosis by Suppressing Filamentous Actin Assembly
- Sensory Neuron-Derived Eph Regulates Glomerular Arbors and Modulatory Function of a Central Serotonergic Neuron
- Analysis of Rare, Exonic Variation amongst Subjects with Autism Spectrum Disorders and Population Controls
- Scavenger Receptors Mediate the Role of SUMO and Ftz-f1 in Steroidogenesis
- DNA Double-Strand Breaks Coupled with PARP1 and HNRNPA2B1 Binding Sites Flank Coordinately Expressed Domains in Human Chromosomes
- High-Resolution Mapping of H1 Linker Histone Variants in Embryonic Stem Cells
- Comparative Genomics of and the Bacterial Species Concept
- Genetic and Biochemical Assays Reveal a Key Role for Replication Restart Proteins in Group II Intron Retrohoming
- Genome-Wide Association Studies Identify Two Novel Mutations Responsible for an Atypical Hyperprolificacy Phenotype in Sheep
- The Genetic Correlation between Height and IQ: Shared Genes or Assortative Mating?
- Comprehensive Assignment of Roles for Typhimurium Genes in Intestinal Colonization of Food-Producing Animals
- An Essential Role for Zygotic Expression in the Pre-Cellular Drosophila Embryo
- The Genome Organization of Reflects Its Lifestyle
- Coordinated Cell Type–Specific Epigenetic Remodeling in Prefrontal Cortex Begins before Birth and Continues into Early Adulthood
- Improved Detection of Common Variants Associated with Schizophrenia and Bipolar Disorder Using Pleiotropy-Informed Conditional False Discovery Rate
- Site-Specific Phosphorylation of the DNA Damage Response Mediator Rad9 by Cyclin-Dependent Kinases Regulates Activation of Checkpoint Kinase 1
- Npc1 Acting in Neurons and Glia Is Essential for the Formation and Maintenance of CNS Myelin
- Identification of , a Retrotransposon-Derived Imprinted Gene, as a Novel Driver of Hepatocarcinogenesis
- Aag DNA Glycosylase Promotes Alkylation-Induced Tissue Damage Mediated by Parp1
- DJ-1 Decreases Neural Sensitivity to Stress by Negatively Regulating Daxx-Like Protein through dFOXO
- Asynchronous Replication, Mono-Allelic Expression, and Long Range -Effects of
- Differential Association of the Conserved SUMO Ligase Zip3 with Meiotic Double-Strand Break Sites Reveals Regional Variations in the Outcome of Meiotic Recombination
- Focusing In on the Complex Genetics of Myopia
- Continent-Wide Decoupling of Y-Chromosomal Genetic Variation from Language and Geography in Native South Americans
- Breakpoint Analysis of Transcriptional and Genomic Profiles Uncovers Novel Gene Fusions Spanning Multiple Human Cancer Types
- Intrinsic Epigenetic Regulation of the D4Z4 Macrosatellite Repeat in a Transgenic Mouse Model for FSHD
- Bisphenol A Exposure Disrupts Genomic Imprinting in the Mouse
- Genetic and Genomic Architecture of the Evolution of Resistance to Antifungal Drug Combinations
- Transposable Elements Are Major Contributors to the Origin, Diversification, and Regulation of Vertebrate Long Noncoding RNAs
- Functional Dissection of the Condensin Subunit Cap-G Reveals Its Exclusive Association with Condensin I
- PLOS Genetics
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle- The G4 Genome
- Neutral Genomic Microevolution of a Recently Emerged Pathogen, Serovar Agona
- The Histone Demethylase Jarid1b Ensures Faithful Mouse Development by Protecting Developmental Genes from Aberrant H3K4me3
- The Tissue-Specific RNA Binding Protein T-STAR Controls Regional Splicing Patterns of Pre-mRNAs in the Brain
Kurzy
Zvyšte si kvalifikaci online z pohodlí domova
Současné možnosti léčby obezity
nový kurzAutoři: MUDr. Martin Hrubý
Všechny kurzyPřihlášení#ADS_BOTTOM_SCRIPTS#Zapomenuté hesloZadejte e-mailovou adresu, se kterou jste vytvářel(a) účet, budou Vám na ni zaslány informace k nastavení nového hesla.
- Vzdělávání



















